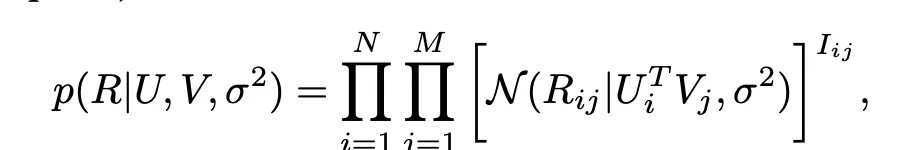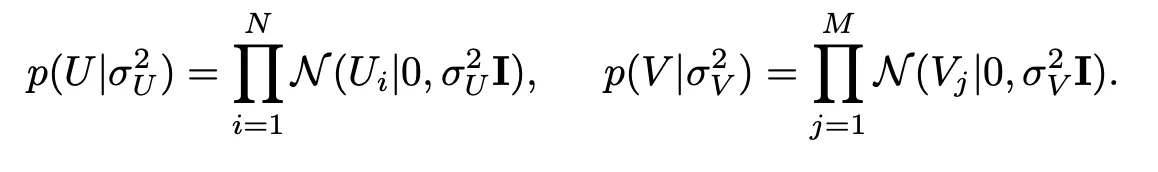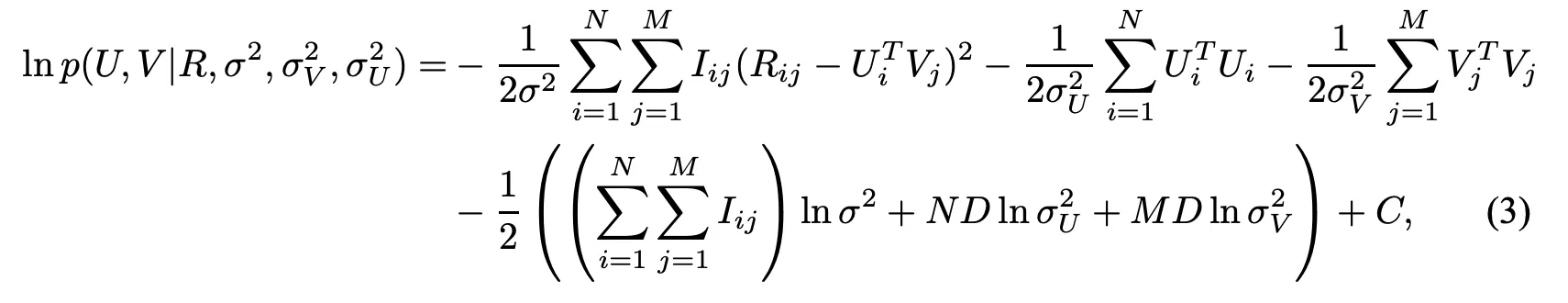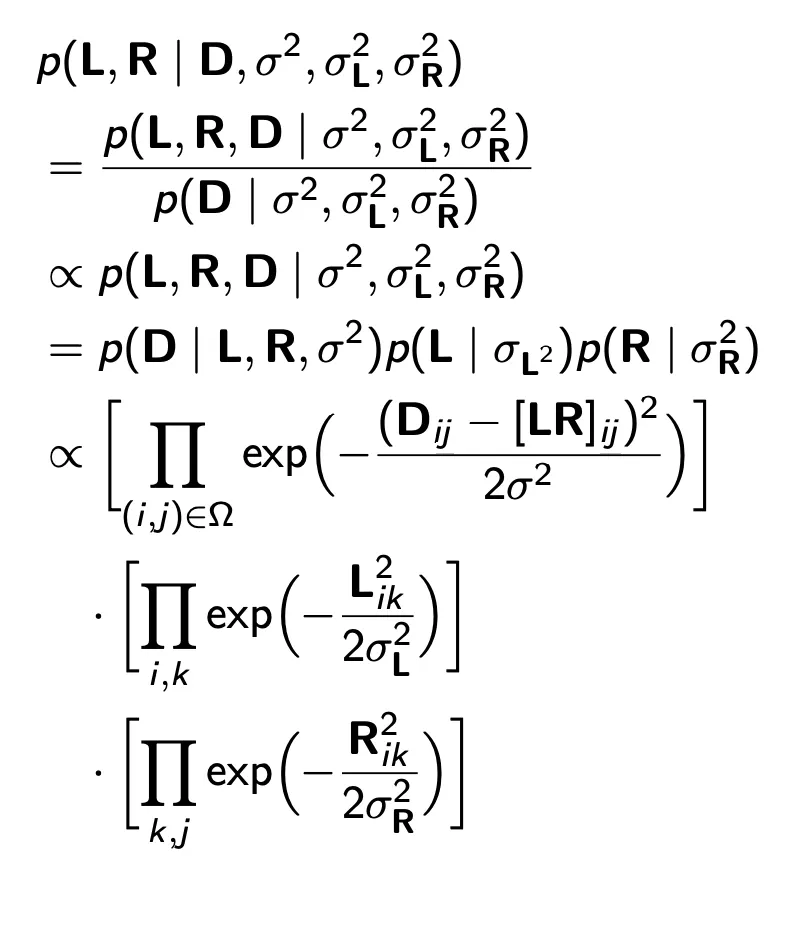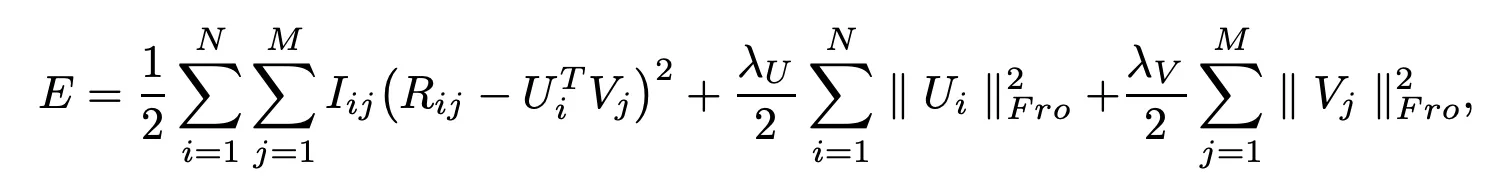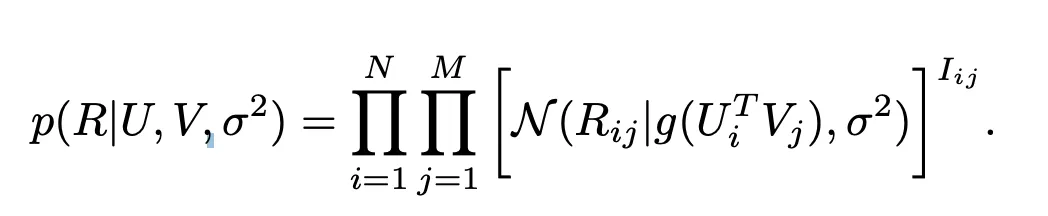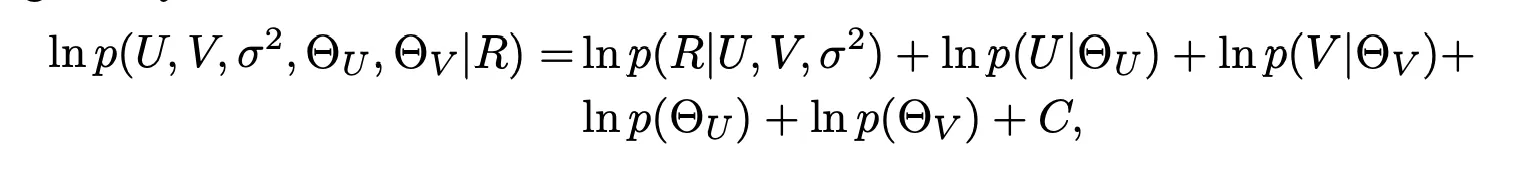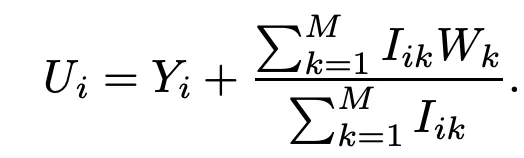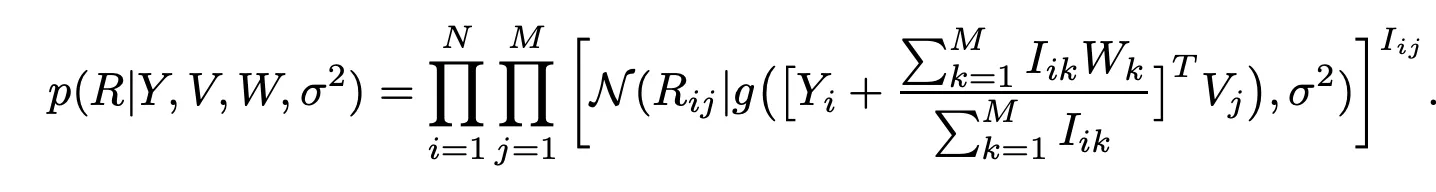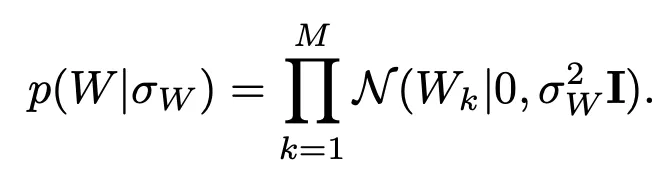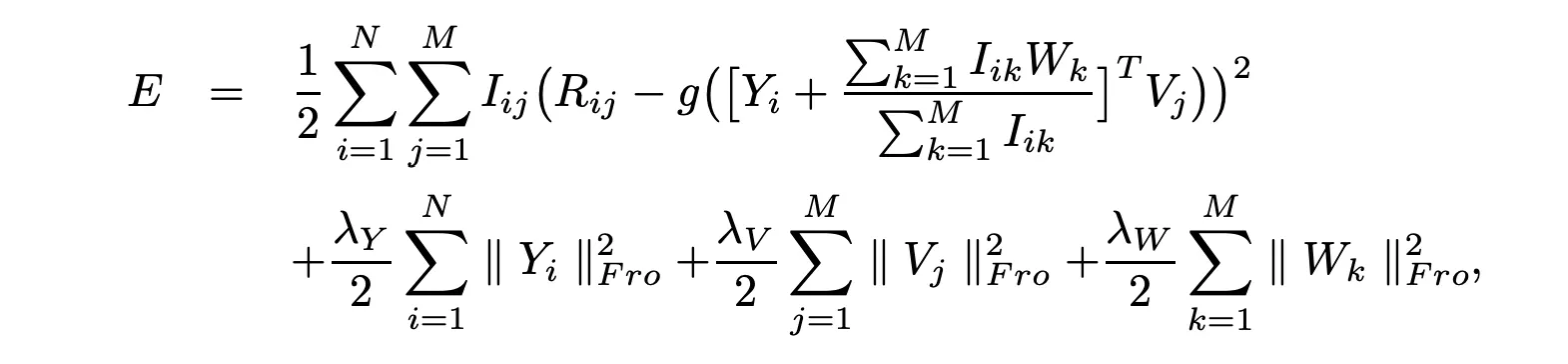Abstract
•
collaborative filtering을 활용하는 접근법들에서 큰 사이즈 dataset과 평가 정보가 거의 존재하지 않는 사용자들은 다룰 수 없다.
•
PMF는 linearly scalable 하고, large, sparse, imbalanced Netflix dataset에 대해서 확장이 가능하다.
•
비슷한 영화에 평가한 유저들은 비슷한 선호를 가지고 있다는 가정 하에 constrained version of PMF를 제안함.
•
굉장히 일반화가 잘 된다.
Introduction
•
여러 Probabilistic model이 제시되었지만 2가지 이유로 잘 안 됨.
◦
large dataset에 scale이 잘 안 됬다.
◦
기존에 존재하는 방법들은 few rating을 가지고 있는 user에 대해서는 rating이 힘들었다.
•
Section2에서 PMF에 대해서 소개
•
Section3 에서 adaptive prior을 포함한 모델로 확장하고, 이런 priors가 model complexity를 자동으로 조절하는지 살펴볼 거임.
•
Section 4에서, constrained version을 소개.
◦
이게 standard SVD 모델을 outperform 함.
Probabilistic Matrix Factorization
U,V,분산이 주어져있을 때, 점수는 예측값이 평균인 정규분포를 띤다고 가정.
U와 V에 대한 latent vector는 평균이 0, 분산이 각각 있는 정규 분포로 가정.
Bayesian posterior을 구하고 ln을 씌우면
결국 gradient descent를 활용할 수 있는 minimize objective function은 다음과 같음
•
일반적인 SVD랑의 차이를 보면 Regularization term이 존재
normal distribution을 가정하기 때문에, prediction이 실제 rating 범위 바깥으로 나갈 수도 있다.
그렇기 때문에 rating value 또한 정규화를 해주고, 예측 값 또한 sigmoid 함수를 통과시켜서 0~1 사이의 범위를 가지도록 해준다.
Automatic Complexity Control
1.
feature matrix의 dimensionality를 줄인다
a.
imbalance한 데이터에 취약하다. row나 column에 대해서 관찰되는 데이터가 불균형이 있을 때. 단일한 차원 수로 하면, 어떤 데이터에 대해서는 너무 낮은 차원이고, 어떤 거에 대해서는 너무 높은 거다.
2.
대신에 lambda를 이용하는 방법이 있을 것이다. 하지만 적절한 lambda를 찾는 것은 cost expensive하다. 이걸 해결하는 방법을 소개함.
대신에 위에 있는 식에 따르면 L2-norm으로 penalizing을 하는게 곧 MAP를 높이는 방식이라고 바라 볼 수 있다. 각 lambda는 U,V에 대한 Sigma로 조절이 되는 값들이다. 따라서 이런 hyperparameter에 대한 prior를 도입해서 모델 complexity를 자동으로 조절할 수 있게끔 한다.
예를 들어 user와 movie에 대해서 spherical priors를 설정함으로써, PMF에 대한 standard form을 자동으로 맞춘다.
따라서 아래와 같은 형태로 hyperparameter를 포함한 MAP를 구성하고 이를 maximizing 하는 식이다.
Constrained PMF
기존 PMF의 경우 User 모델을 평균 0, 분산이 존재하는 gaussian으로 모델링함. 하지만 이러면 개인화가 일어나지 않고, 전체 유저의 평균적인 취향을 반영하는 문제가 야기 됨.
이에, 적은 수의 평점을 남긴 유저는 평점을 남긴 영화를 이용해서 prior를 가정한다. W_k는 학습되는 값이며, latent similarity constraint matrix 이다. W 매트릭스의 i번째 열은 유저가 평점을 남긴 특정한 영화가 해당 유저의 feature vector의 평균에 주는 영향을 잡아낸다.
Y_i는 해당 평균에서 떨어져있는 offset을 얘기함.
Unconstrained에 대해서는, U_i랑 Y_i가 같다. 왜냐하면 prior mean이 0으로 고정되있기 때문임.
따라서 conditional distribution은 다음과 같이 된다.
W에 대한 prior는 zero-mean spherical gaussian prior를 따른다고 가정함.
다음 objective function을 minimize 하는 문제로 바뀐다.
Experiments
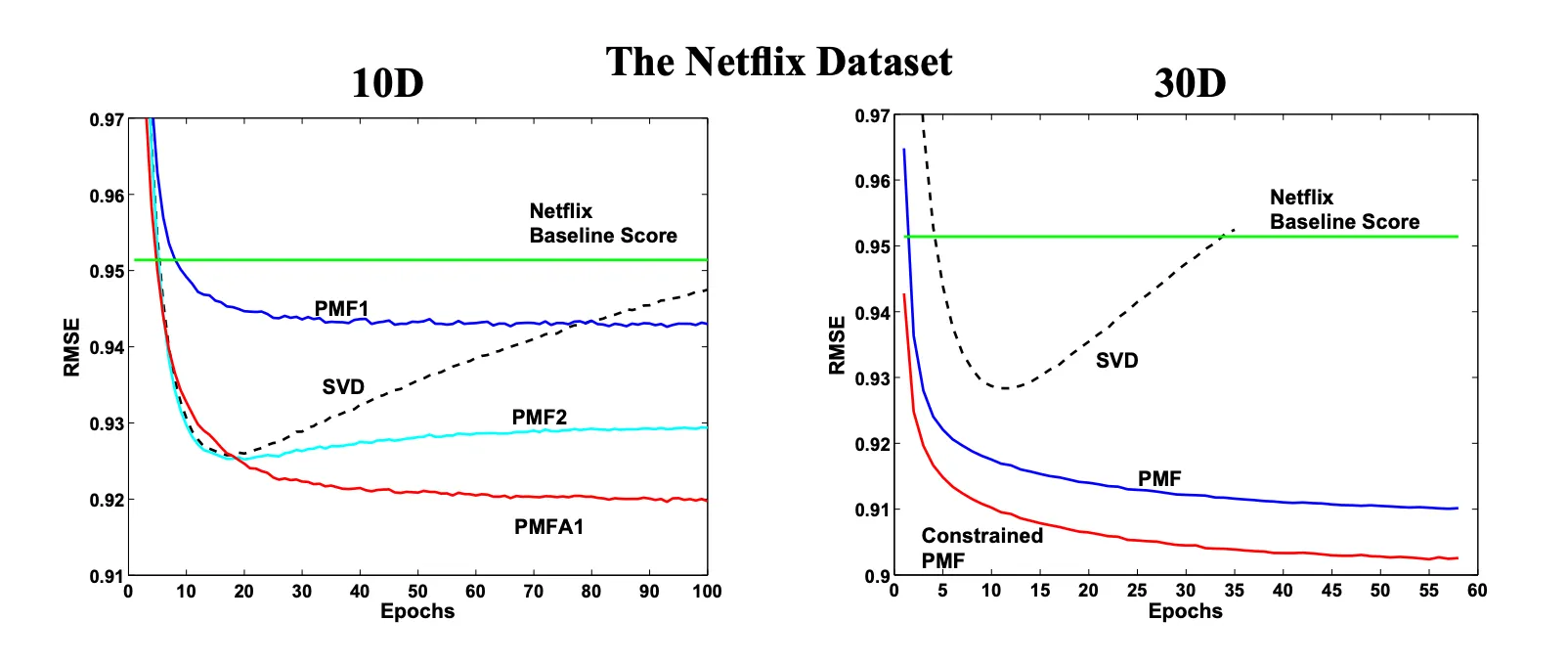
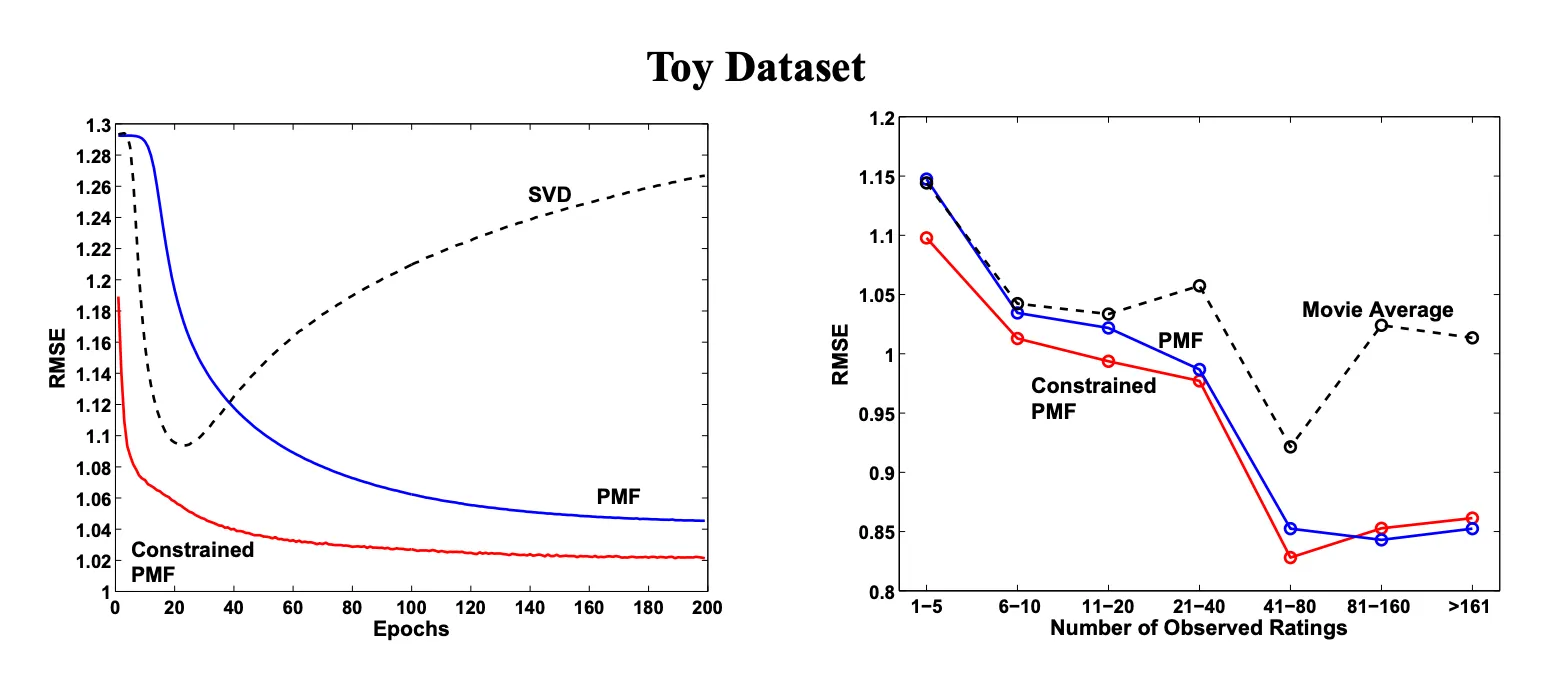
sparse 한 데이터셋에 대해서도 constrained PMF가 더 좋은 성능을 보임.
기록한 평점의 수가 20개 미만일 때는 constrained PMF가 더 좋은 성능을 보이다가 그 이상이 되면 큰 차이를 안 보임.