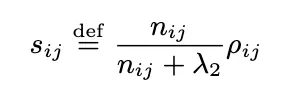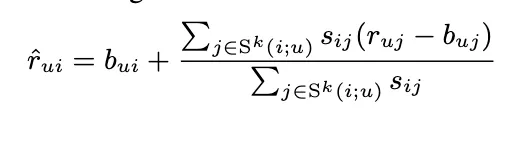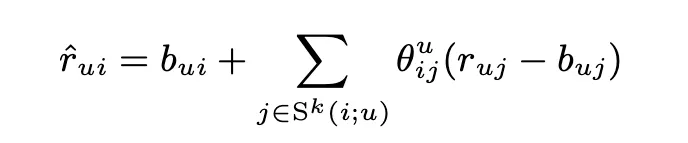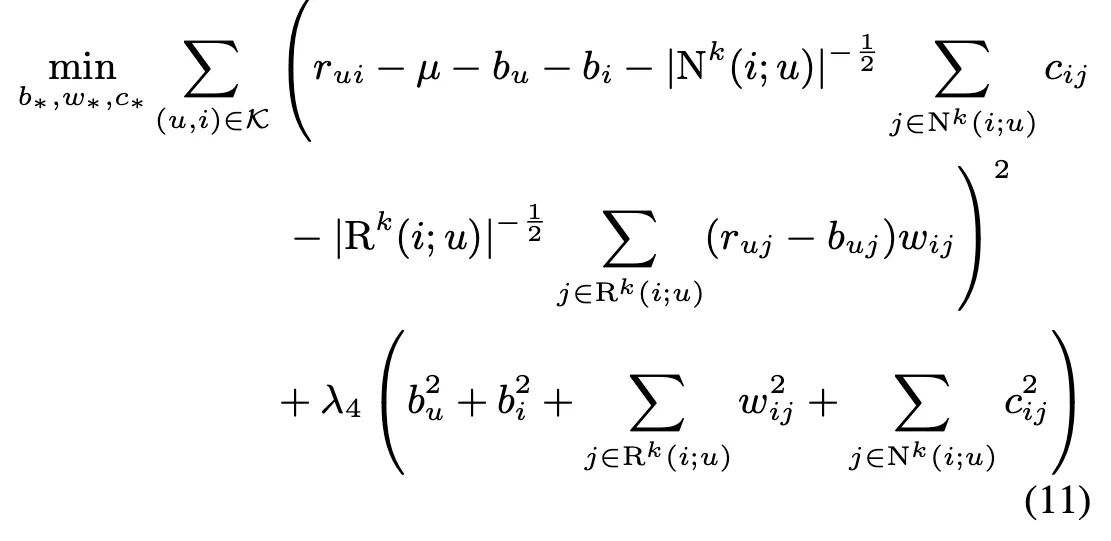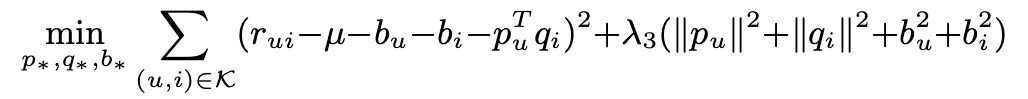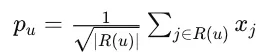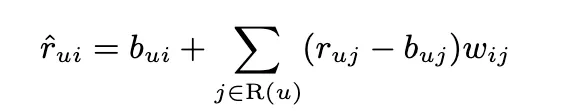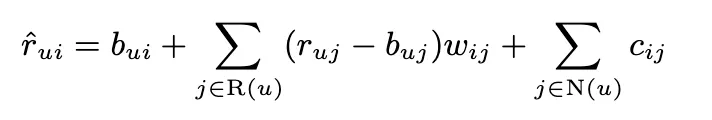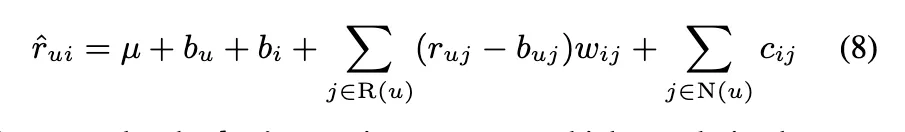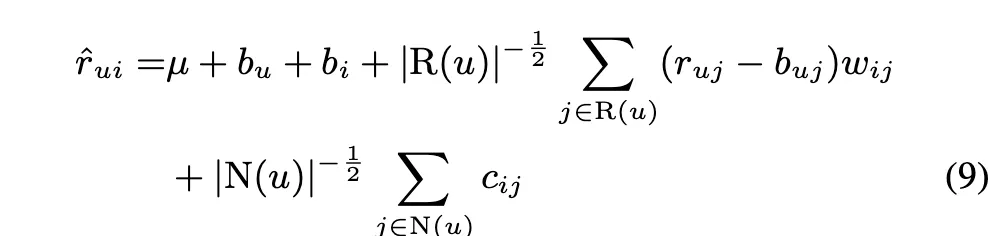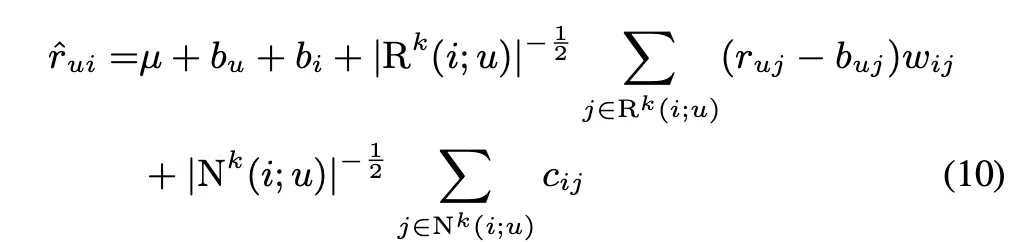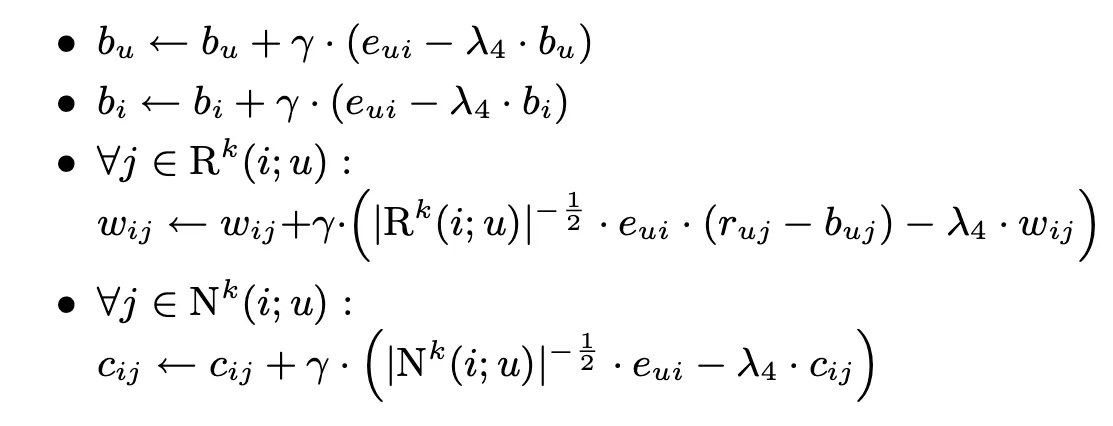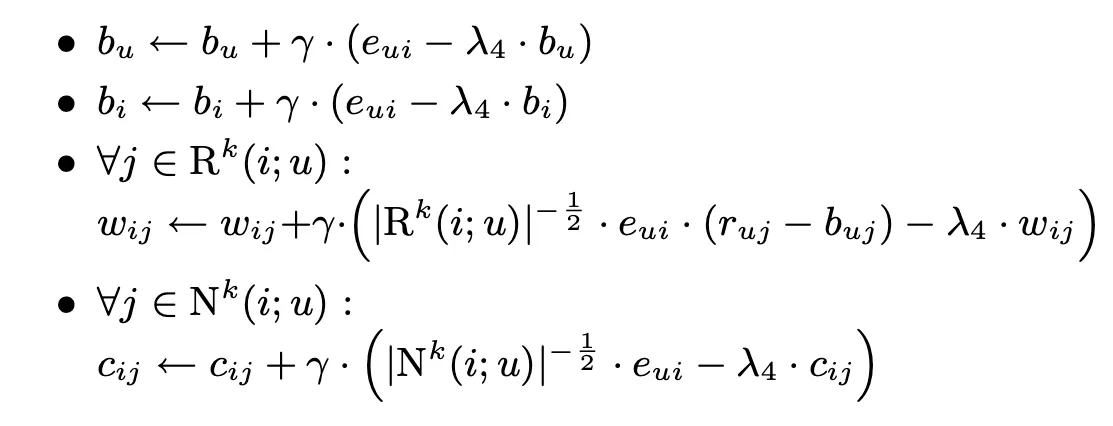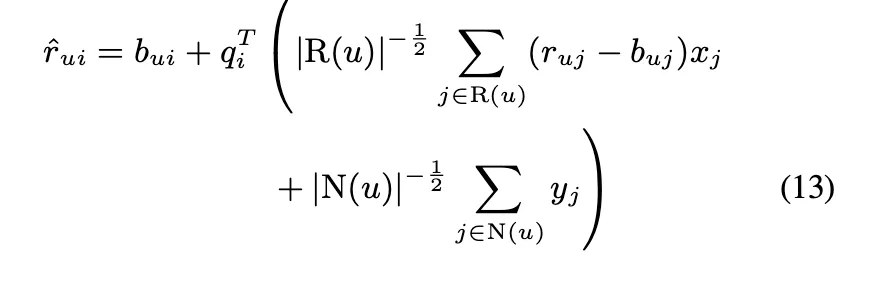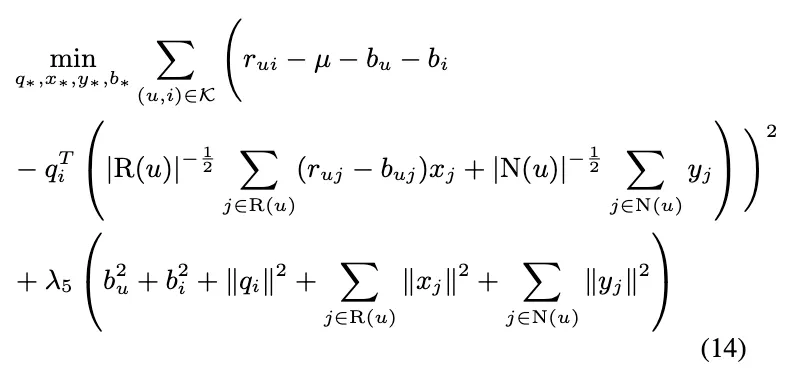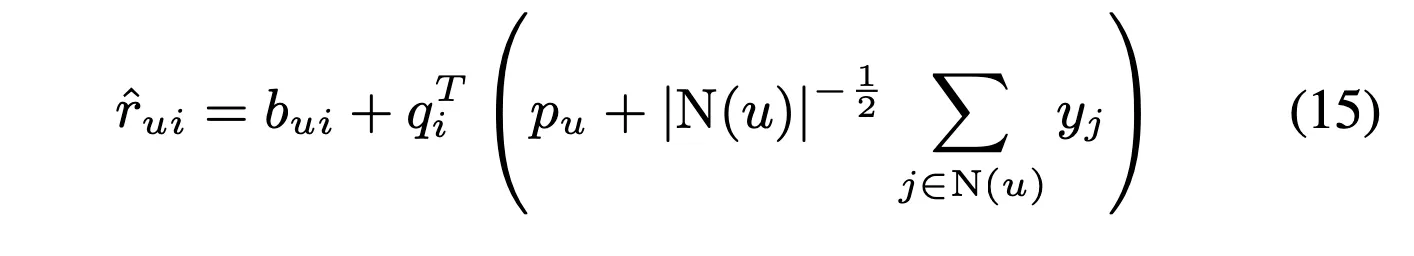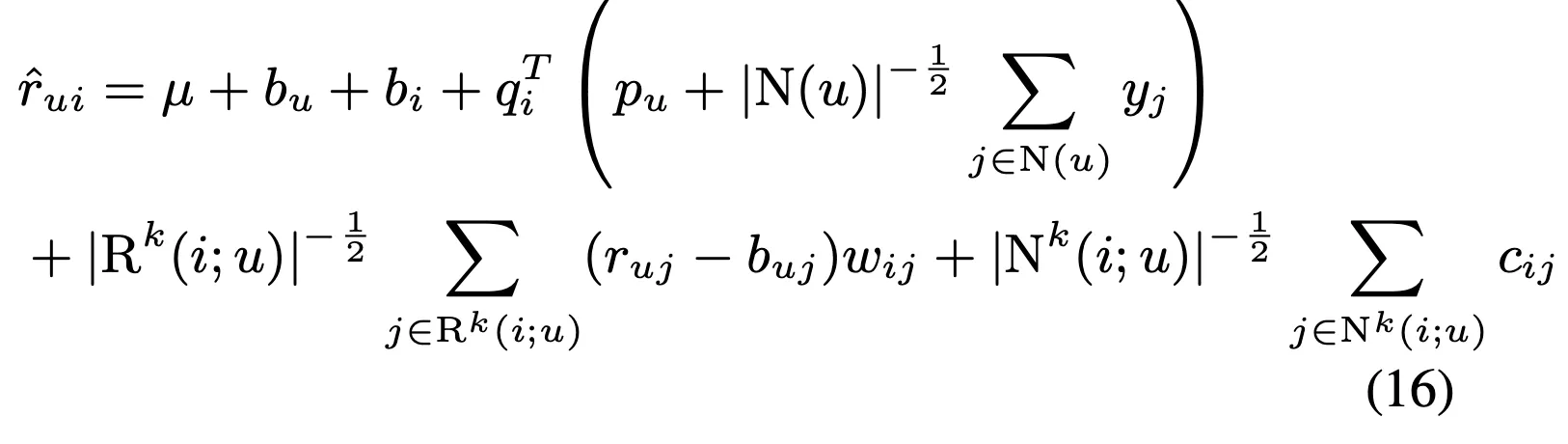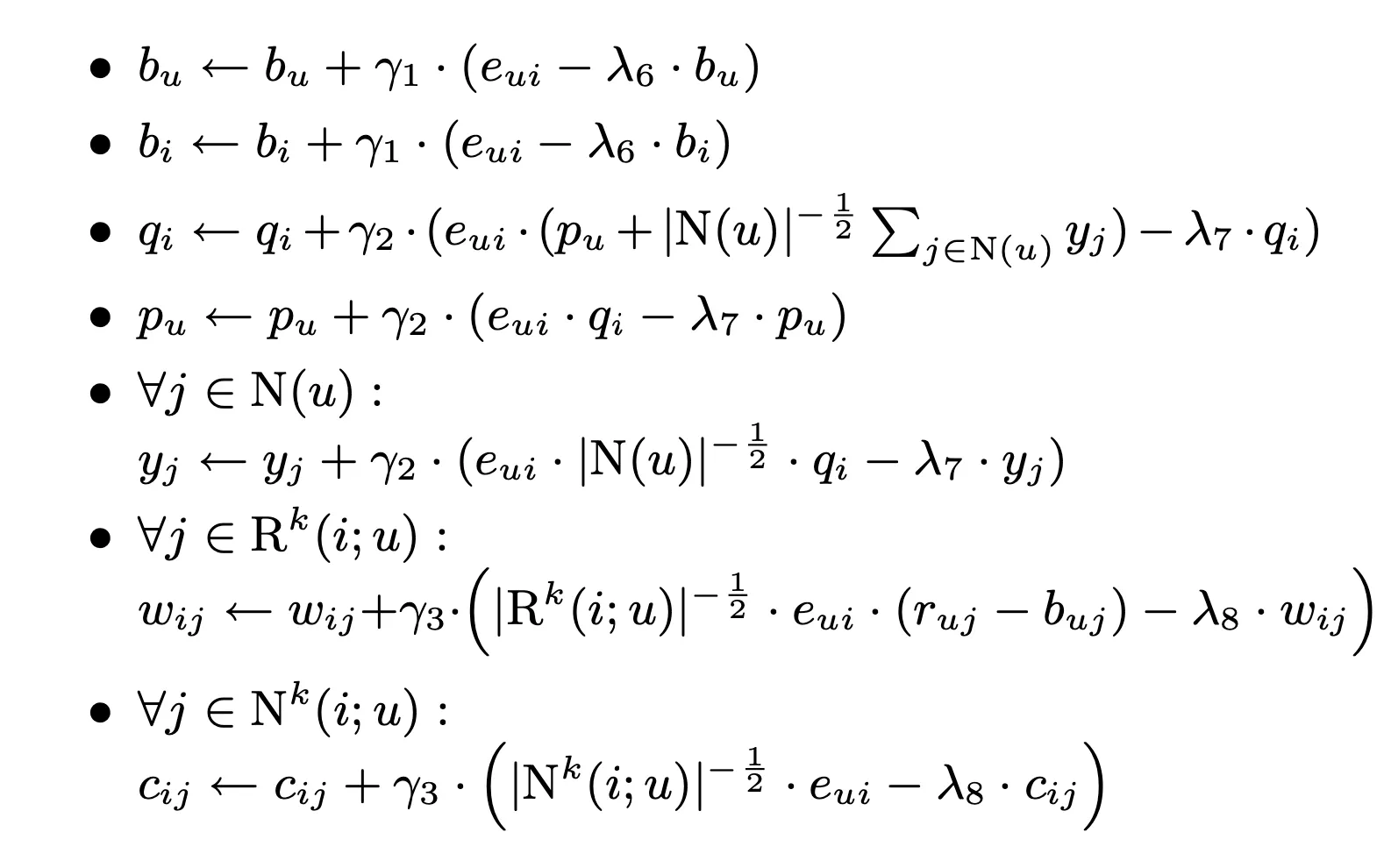neighborhood 방법에서 userspecific한 유사도 찾기를 버리고 gradient descent를 통해 global한 관계 weight를 발견하고자 함.
latent factor의 경우에 implicit data를 포함한 모델 개발을 통해 성능 향상을 이룸.
neighborhood 방식 + latent factor 방식을 결합해서 낮은 RMSE를 달성
Abstract
•
Collaborative Filtering의 두 가지 모델인 Latent Factor 모델과 Neighbor hood model을 결합한 것이다.
•
Latent Factor 유저와 상품을 프로파일화해서 사용자 피드백으로부터 자동으로 추론된 요인을 기반으로 평가를 설명.
•
neighbor hood model은 유사성을 분석하는 것이다.
Introduction
•
Neighborhood method
◦
item 간 또는 유저 간 관계를 계산하는 것이 초점임.
◦
아이템 기반의 접근은, 유저의 선호를 그 사람이 평가한 비슷한 아이템들로 채우는 것이다.
◦
이 방법은 사용자를 아이템 공간으로 옮기는 것임. (평가한 아이템의 basket으로 옮기는 것)
◦
localized relationship을 detecting 하기에 효과적이다.
◦
강력한 neighborhood relationship을 찾는 것에 집중하고, 평가의 주된 이유는 무시하는 경우가 있음. 모든 유저의 평가에 있는 약한 시그널은 캡쳐하지 못한다.
•
Latent factor model
◦
User랑 Item을 같은 latent space로 변환한다. 그래서 직접적인 비교가 가능함.
◦
대부분의 아이템에 대해 동시에 연관이 있는 전반적인 구조를 추론하는데 효과적임.
◦
굉장히 가까운 그런 관계에 대해서 detection은 다소 약하다.
Preliminaries
Baseline Estimates
사용자 u에 대한 편향 + i에 대한 편향 + 전체적인 편향 = b_ui이다.
이걸 찾는 과정은 least squares problem을 풀면 된다.
Neighborhood models
•
user-oriented → item oriented로 넘어감.
•
item 간의 유사도를 측정하는 것이 중요하다.
•
Pearson corelation coefficient를 이용해서, item i와 j를 유사하게 평가하는 경향을 측정함.
•
많은 레이팅이 불분명하기에, 몇 몇 아이템은 공통 평가자가 거의 없을 수 있음.
•
유사도 측정
•
rating 추정
◦
average sum of similar set K
◦
이렇게 하면 neighborhood information이 없는 경우 문제가 됨.
◦
interpolation weights를 유도해서 집어넣는게 좋음
interpolation weights는 item rating 간의 inner product로 추정함.
Latent factor model
사용자는 p_u로 나타내어지고 item은 q_i로 나타내어짐.
NSVD 모델이 제안되었는데, 이건 각 유저를 바로 표현하는게 아니라, 아이템의 집합으로 표현하는 것이다.
Implicit Feedback
1,0 등 평가하고 싶다 아니다 등의 의견을 내는 것 또한 Implicit data라고 판단했고, 이걸 결합하는게 성능 향상에 도움이 됨. 이런 것들은 모든 레이팅 데이터에 본질적으로 들어가있는 데이터임.
Neighborhood Model
interpolation과 다른 점은 기존에는 item i에 대해서 비슷한 item 집합 K에 대해서 보간법을 진행했다면, 이건 user가 평가한 전체에 대해서 item i와 관련된 정도를 w_ij로 직접적으로 예측한다는 것.
기존에 사용된 s_ij는 user-specific 유사도이다. 이걸 버리고 전역적인 w_ij를 도입함.
해당 모델은 implicit data를 항에 넣은 것.
r_ui - b_ui를 보간하는 건 r_uj-b_uj에서 왔기 때문에 b_ui 값과 b_uj 값이 호환성이 있어야한다. 하지만 우리는 interpolation을 쓰는게 아니기 때문에 b_ui랑 b_uj를 decoupling 할 수 있다.
지금 모델은 인풋을 많이 넣은 사용자에게는 좀 더 risk를 감수하고, 그렇지 않으면 safe estimates를 해준다.
하지만 이렇게 많이 평가하는 사람이랑, 그렇지 않은 사람에 대해서 점점 격차가 많이 벌어져서, 그 크기를 좀 조정하려고 함.
계산 복잡도를 줄이기 위해서, 유저가 평가한 아이템 전부에 대해서 sum을 하는게 아니라 관련 있는 것 중에서 평가한 것들에 대해서만 계산을 진행함.
최종적인 식은 다음과 같음
다음은 update rule
Latent Factor Models Revisited
•
기본적으로 Patrek의 모델을 차용함. 유저가 소비한 아이템의 합을 표현할 때, Neighborhood에서 사용한 방법을 이용해서 표현함.
•
각 아이템 i는 q_i, x_i, y_i로 표현이 됨.
•
유저에 대한 파라미터를 제공하지 않더라도, 아이템만으로 유저를 표현할 수 있다.
•
이렇게 하면 좋은 점
◦
적은 파라미터를 사용한다.
◦
유저를 파라미터화 하지 않기 때문에, 새로운 유저가 와서 시스템에 피드백을 주면 모델을 re-train할 필요 없이 새로운 파라미터를 추정하면 된다. 유저의 선호를 업데이트하기 위해 새로운 레이팅을 이용할 수 있다.
◦
설명력이 올라간다.
◦
implicit feedback을 효과적으로 통합한다.
▪
피드백 양에 따라 어떤 피드백이 더 중요한지 결정된다.
▪
explicit이 implicit보다 중요할텐데, 이에 대한 conversion 비율을 x_j랑 y_j로 자동으로 조절한다.
학습 시에는 아래와 같은 최적화 식으로 함
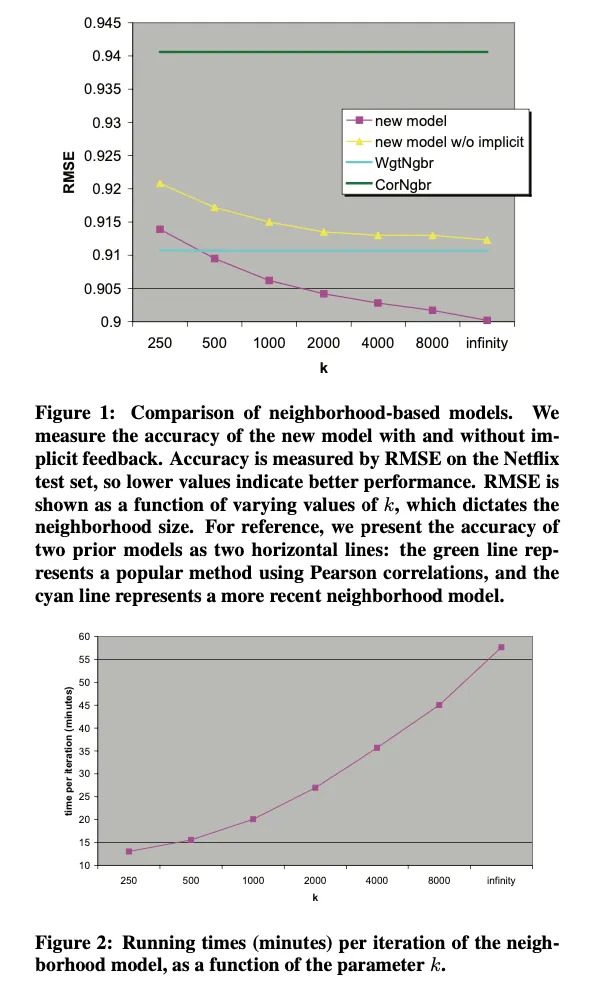
결과의 경우 SVD보다는 살짝 좋음. 아마 이거는 Implicit feedback 때문임.
근데 아마 좀 더 명확한 implicit data가 있으면 좋지 않을까? 싶음.
결국 implicit data가 중요하기 때문에 implicit data만 추가한 모델을 생각해볼 수 있음. 이게 SVD++이고, 이거는 asymmetric SVD에서 누리는 이점은 누리지 못한다. SVD++이 성능이 제일 좋음.
Integrated Model
neighborhood 모델을 SVD ++과 합쳐보려고 함.
1st tier: 영화와 유저에 대한 일반적인 특성을 나타냄
SVD++ 항: user과 item profile의 interaction을 나타냄.
neighborhood 항: fine grained adjustments를 나타냄. Joe가 Signs와 관련된 영화를 낮게 평점을 줬다 등
Evaluation
10% 향상된 RMSE가 실제로 추천 경험을 크게 향상시킬까?
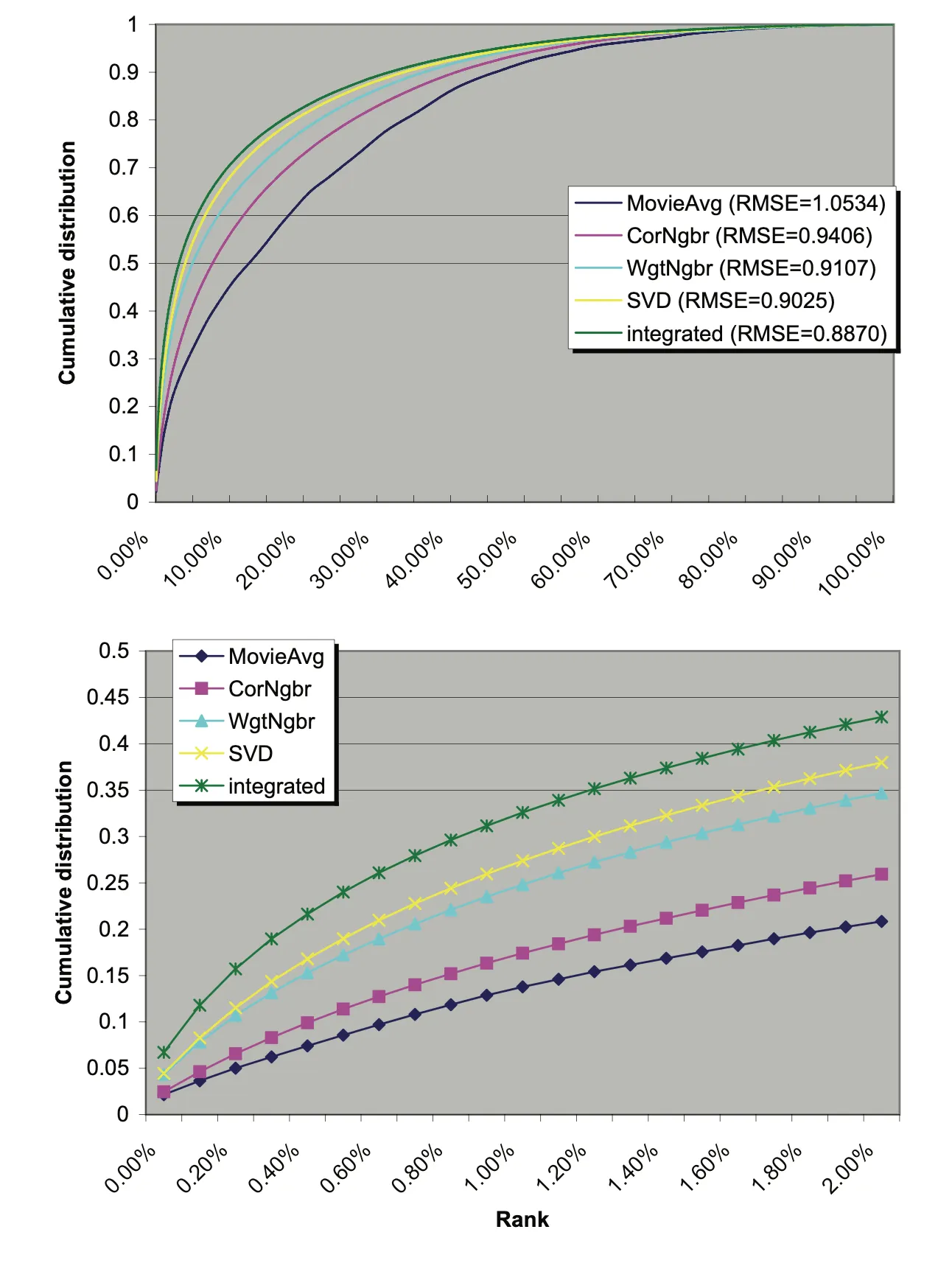
top K recommendation으로 테스트를 해봄.
각 영화 i에 대해서, 5점을 받은 u가 있다고 할 때, 우리는 u에 의해 평가를 받은 다른 1000개의 영화를 임의로 뽑고, 이 1001개에 대해서 rating을 시킨다. 가장 높은 예측이 높은 게 추천이 된다. 그런 경우 우리는 이게 5점을 받은 그 영화이기를 바람.
최선의 경우, 아무것도 이 i보다 순서상 먼저 오지 않을 것이고, 최악의 경우 이 i보다 전부다 앞에 올 거다.
아래 그래프에서 x축은 1000개 중에 몇 프로를 추천해 쓸 것이냐이고, y축은 5점을 맞은 친구가 들어올 확률을 의미함. 어차피 엄청나게 많은 후보군을 줄 수 없기 때문에 2% 정도로 줄여서 그래프를 비교해보면 integrated 모델이 가장 좋음. 예를 들어 0.2%만 추출해서 추천한다고 할 때 0.157이라는 숫자가 0.1이나 0.05보다는 많이 좋음.