Index And Hashing

Secondary Index

paramters & 구조

Static & efficiency

Index

Dense

모든 레코드마다 index가 하나씩 다 달려있는 상태

•

이게 왜 좋냐?

◦

index block의 숫자는 data block보다 더 작다 → key랑 포인터만 있으니까

◦

Key는 정렬되어있고 binary search를 할 수 있다

◦

index는 메모리에 들어갈만큼 작다.

Sparse

block마다 key-pointer pair가 달려있는 상태

dense보다 더 적은 공간을 차지하지만, record 찾는데는 시간을 더 쓴다.

전체 n개의 record가 있을 때, 한 개의 block은 3개 레코드를 가지거나 10개의 key-pair 포인터를 가진다.
데이터 파일 + dense index: ceiling(n/10){인덱스} + ceiling(n/3){데이터 파일}
데이터 파일 + sparse index: celing(n/30){인덱스} + celing(n/3){데이터 파일}
Markdown
복사

Multiple Level

index 파일이 여전히 크면 추가적인 레벨이 dense 이거나 sparse여야하나?

•

sparse여야한다. dense여봐야 소용이 없다.

•

블럭에 대한 reduction이 없기 때문이다.

Secondary Index

•

primary index와 다르게, 레코드의 위치를 결정하진 않는다.

•

random한 order로 되어있기 때문에

sparse index에서 정렬이 되어있다하더라도, 어차피 해당 block 내에서 정렬이 안 되어있기 때문에 찾을려고 하는 값이 어디있는지 알 수 없다. (sparse는 블럭 별로 하기 때문에 정렬이 안 되어있으면 그 블럭을 따라가더라도 값이 그 안에 무조건 있을지 확신할 수 없음) 따라서 무조건 dense가 되어야한다.

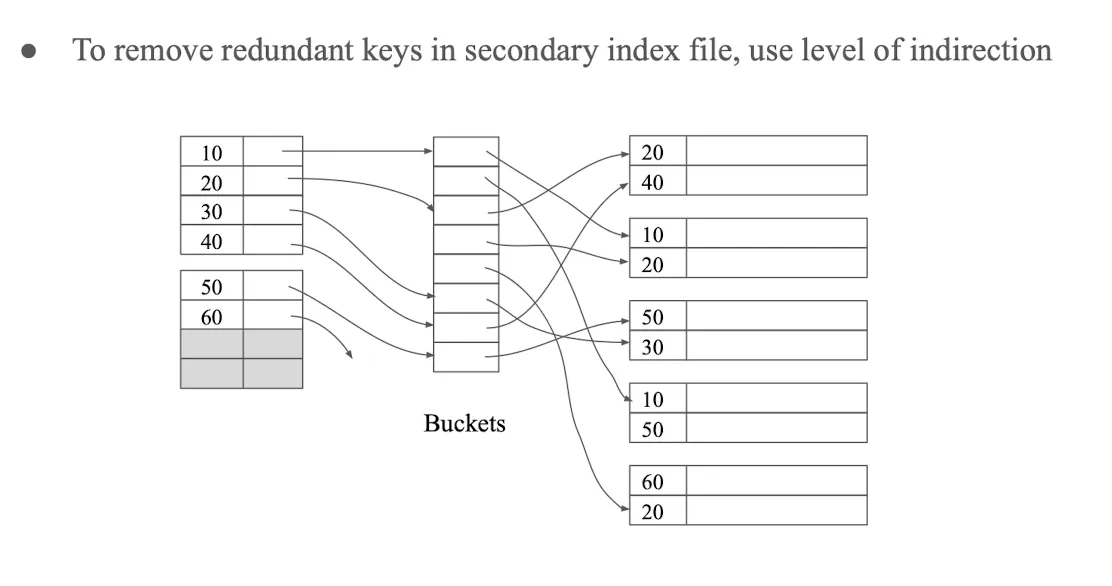
redundant key를 막으려면, multiple level을 적용하면 된다.

•

언제 좋느냐

◦

clustered file 구조에 적합함

SELECT title, year
FROM Movie, Studio
WHERE presC# = zzz AND Movie.studioName = Studio.name;
Markdown
복사

◦

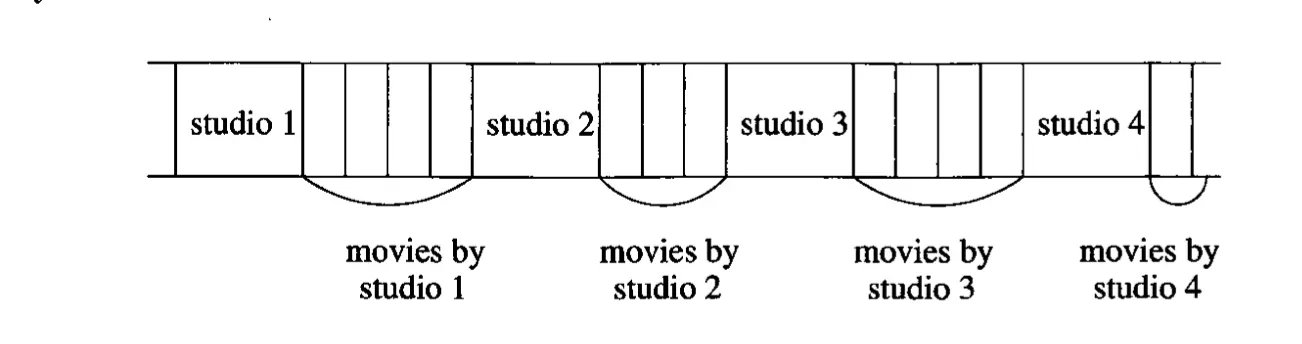
이런 쿼리가 빈번하게 일어난다면, clustered file 구조가 유리하다.

◦

위의 그림과 같은 구조로 clustered 될텐데, 이런 경우 studio에 대해서 presC#에 대해 secondary index를 만드는 것이 좋을 것.

◦

물론 그에 딸린 movies에 대해서도 index가 걸려있어야, 쉽게 찾을 수 있을 것

◦

key가 포인터보다 크고 key가 평균적으로 두 번 등장할 때

▪

이렇다면 indirection을 이용해서 unique하게 만들 수 있기 때문

◦

대부분의 레코드를 보는게 아니라 bucket 포인터만 사용할 수도 있다.

▪

select title from movie where studioName = ‘Ghibli’ and year = 2008;

▪

이 경우 대해서 studioName과 year에 대해 secondary index가 있다면 겹치는 부분만 생각하면 된다.

Inverted Index

•

앞의 아이디어가 text 정보를 뒤질 때 사용됨.

•

‘cat’과 ‘dog’라는 정보를 가지고 있는 document를 찾고 있다해보자

•

cat, dog에 대해서 어떤 doc에 등장하는지를 다 가지고 있으면, 그 교집합도 쉽게 찾을 수 있을 것

B-Tree

paramters & 구조

각 block은 n개의 search key와 n+1개의 포인터가 있다.

•

Rule

◦

leaf node의 key들은 data file로부터온 keys의 복사본이다. 이 키들은 leaf에 대해서 왼쪽에서 오른쪽으로 sorted가 되어있다.

◦

root에서, 최소 2개의 포인터가 사용되어야한다. 모든 포인터들이 바로 아래 단계의 B-tree 블럭을 가리켜야한다.

◦

leaf에서 마지막 포인트는 그 다음 leaf block을 가리켜야한다. leaf block에 있는 n개의 포인터들 사이에서, 최소 (n+1)/2의 버림만큼의 포인터는 사용이 되어야한다. 사용되지 않은 애들은 null이고 아무곳도 가리키면 안 된다.

◦

중간 노드에 대해서는 n+1개의 포인터가 아래 레벨 블럭을 가리키는데 사용될 수 있다. (n+1)/2 올림만큼이 최소한으로 사용이 되어야한다.

◦

K번째 pointer에 대해서는 K-1 key ≤ keys ≤ K key

•

pointers and keys

Node type	Min #pointers	Max #pointers	Min #keys	Max #keys
Interior	(n+1)/2 올림	n+1	(n+1)/2 올림 -1	n
Leaf	(n+1)/2 내림	n+1	(n+1)/2 내림	n
Root	2	n+1	1	n

◦

Interior

▪

n+1개의 pointer가 전부다 아래쪽을 가리키는데 쓰이니 n+1/2 올림으로 계산

▪

min key의 경우, key값 자체가 pointer보다는 하나가 작으니 1을 빼준다.

◦

Leaf

▪

마지막 포인터가 항상 그 다음 노드를 가리키고 있으니 전체의 절반의 버림 처리를 해줘야함.

▪

Min key 같은 경우에 key값과 포인터가 항상 특정 블럭을 가리키도록 같아야하므로 Min Pointers과 Min keys는 그 숫자가 같아야함.

◦

Root

▪

Root의 경우 최소한 두 개로 나뉘기는 해야하니 Min pointer값이 2이고 이에 따라 Min key값은 1이다.

▪

다만 record가 1개인 경우에는 실제로 한 개가 있을 수도 있다.

Look up

•

값 찾기

◦

그냥 binary search로 가면 된다.

•

범위로 찾기

◦

a≤ x ≤ b인 경우에 a가 있든 없든 a보다 크거나 같은 첫 leaf로 간다음 b보다 크지 않다면 다음 노드로 이동함.

◦

범위가 한 방향인 경우 a≤ x 인 경우에, a보다 크거나 같은 친구부터 끝까지 간다.

Insertion

•

적절한 leaf에 넣는다. room이 있으면 넣음

•

room이 없다면, leaf를 반으로 쪼갠다. 각각 half-full이거나 half-full을 막 넘는다.

•

node를 쪼갠다는 건, 바로 위 레벨에 새롭게 생긴 친구를 가리킬 key-pointer pair가 필요하다는 말. 따라서 그 위의 레벨에 집어넣는 것을 똑같이 반복함.

•

예외적으로 root에 넣는데, room이 없다면, root를 쪼개고 새로운 higher level을 넣는다.

•

split node를 하고 부모에 집어넣을 대, key 관리를 잘 해야한다.

•

N이 leaf node이고, capacity가 n일 때

◦

n+1째 key를 넣으려고 함.

◦

new Node M

◦

첫번째 올림(n+1/2)가 N에 들어가고 나머지는 M으로 간다.

•

N이 interior node이고, capacity가 n일 때

◦

N에 대해서 n key가 있고 n+1 pointer가 있을 때, 위에서 쪼개져서 막 하나가 올라왔다. n+2 포인터가 됫음

◦

M을 새로 만들고.

◦

첫 올림((n+2)/2)만큼을 N에 남겨놓고, 남은 버림((n+2)/2) 만큼을 M으로 옮긴다.

◦

올림(n/2) key를 N에 남겨놓고, 버림(n/2) key를 M으로 옮기면 딱 하나가 남음.

◦

이 하나는 M의 자식들 중 첫번째에 갈 수 있도록 하는 key이다. 이 key가 N이나 M에 나타나지 않더라도 M에 있어야한다. K는 N의 부모와 M에 추가된다.

Deletion

•

삭제했는데, 해당 노드의 유지가 더 이상 어려울 때 두 가지 방법이 있음

•

1번

◦

N에 인접한 sibiling 중 하나가 mnimum number보다 많은 키를 가지고 있으면, key-pointer 페어 하나만 들고온다. 

◦

아마 N의 부모에 있는 key들 또한 조정되어야할 것.

◦

N,M에 대해서 M이 right of N일 때, 옮겨지는 key는 아마 가장 작은 key일 것이다. 새로운 M을 반영하기 위해 parent of N,M의 키가 바뀌어야할 것.

•

2번

◦

인접한 sibiling에서 제공해줄 수 없을 때이다.

◦

이 때는 sibiling 끼리 합치면 된다.

◦

부모의 key를 조정하고 parent에 있는 key-pointer를 삭제하면 된다. 만약 충분하면 상관없는데, 아니라면 parent에 대해 똑같이 적용하면 됨

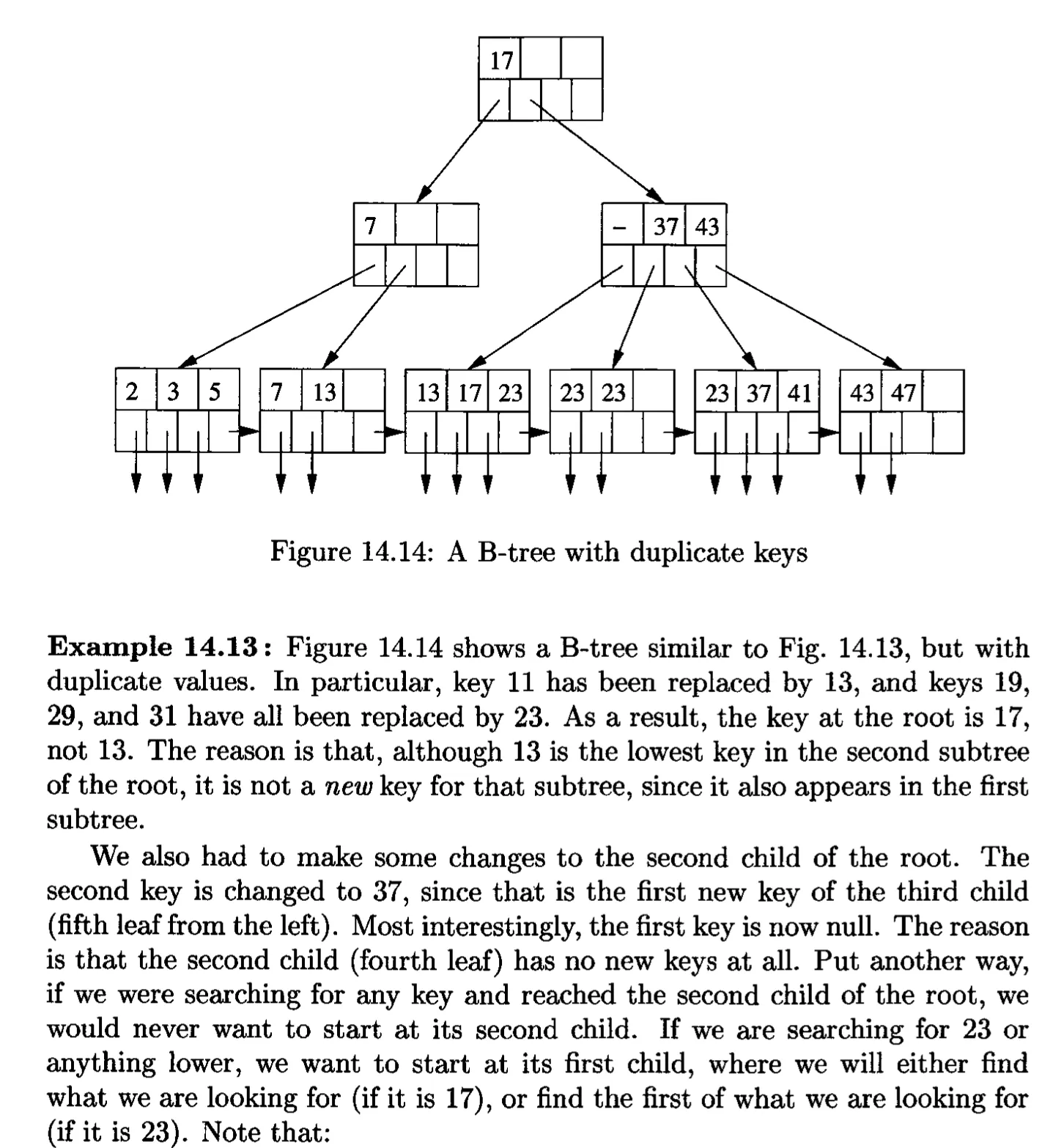
Duplicate Keys

•

정의를 약간 바꿔야한다.

•

new key

◦

Ki에 대해서 i+1번 째의 subtree에는 최소 하나 존재하는데, 그 왼쪽에 있는 subtree에 대해서는 하나도 존재하지 않는 경우가 해당됨

◦

Ki가 null로 되는 경우가 있다.

▪

그에 해당하는 포인터들은 여전히 필요하다. 왜냐하면 오직 하나의 key value를 가지고 있는 트리에 중요한 portion을 차지하기 때문이다.(???)

▪

23보다 작은걸 찾으려고 할 때 root의 두번째 child로 일단 올거다. 그리고 그것의 두 번째 child에서 시작하고 싶지는 않다. 왜냐하면 첫번째 key가 Null이기 때문에 두 번째 child에는 새로운게 없다는 뜻이기 때문.

▪

만약 위의 예시에서 24부터 26까지를 찾는다고 한다면 왼쪽에서 세번째노드, 그니까 첫번째 child로 바로 갈거다. 위와 같은 이유로. 그렇게 해서 찾고자 하는 값이 없다면 사실 오른쪽으로 가볼 필요가 없다. 왜냐면 첫 key가 null이라서 그 다음꺼에는 새로운게 없을 거라는 확신이 있기 때문이다.

▪

만약에 우리가 찾는게 있었다면 null이 아니라 새로운 값이 Key로 박혀있었어야하고, 만약에 다섯번째 leaf에 있었다면 37 대신 그 값이 박혀있었을 거다.

▪

렉처노트 예시

•

만약에 24를 찾는다고 하면, 일단 두 번째 interior 노드로 감

•

첫 번째가 null이고, 두 번째가 37임.

•

따라서 17부터 37 사이에는 new key가 없음

•

따라서 첫 번째 리프에 갔을 때, 24가 없다면 두번째 리프에서부터 시작하는 새로운 키가 없기 때문에 null이 들어가있는 것이므로 두 번째 리프 그 이후를 볼 필요가 없음. (모든 값들이 첫 번째 리프에서 들어가있다는 뜻). 따라서 안 봐도 없다는 걸 알 수 있음

Efficiency

•

B-tree reorganization은 negligible 하다.

•

number of I/O = tree level + one or two for record manipulation

•

root block은 영원히 메모리에 남겨놔야 save I/O 할 수 있다.

Hash Table

1.

block이 consecutive on disk

2.

main memory array of pointers를 사용 ⇒ consecutively하게 저장할 필요 없음

Static & efficiency

•

버킷 수 고정

•

버킷에 레코드가 많으면 overflow qkftod

•

Insertion

•

Deletion

•

Efficiency

◦

enough bucket이어서 한 블럭에 들어가길 원함. 체이닝 없이

◦

그러면 Lookup은 1 disk I/O 이다.

◦

Insert/Delete ⇒ 2 I/O

◦

파일이 grow할 때, long chain이 생김

Extensible

•

첫 i bit를 사용한다.

•

bucket에는 블럭에 대한 포인터가 있음

•

Insertion  & Deletion

◦

Deletion에 대해서는 Insertion의 거꾸로인데, merging하는 건 optional 임

•

Handling duplicated key

◦

splitting으로는 해결을 못하는 거고, overflow block을 사용해야한다.

•

요약

◦

bucket에 메모리 안에 들어간다면 1 disk I/O

◦

약간의 공간적 소비를 하고 full reorganization은 피한다.

◦

double bucket array는 비싸다.

◦

splitting이 블럭당 레코드 수가 작으면 자주 일어나고

◦

어떤 포인트에서 bucket array가 memory에 딱 맞지 않을 수 있다.

Linear Hashing

•

last i bits를 사용함

•

bucket을 추가했는데, 재배치할 때 적당한게 없으면 그대로 있는다.

•

찾을 때 자릿수에 대해서 다 맞는게 없으면 한 자리씩 줄여가면서 찾는다.

•

little wasted space를 하면서 grow & avoiding full reorganizations할 수 있다.

•

extensible array에 비하면 array of bucket이 없다.

•

long chain of overflow가 생길 순 있음

Indexing이 range 검색에는 좋고, Hashing이 Equality based 검색에는 좋다.