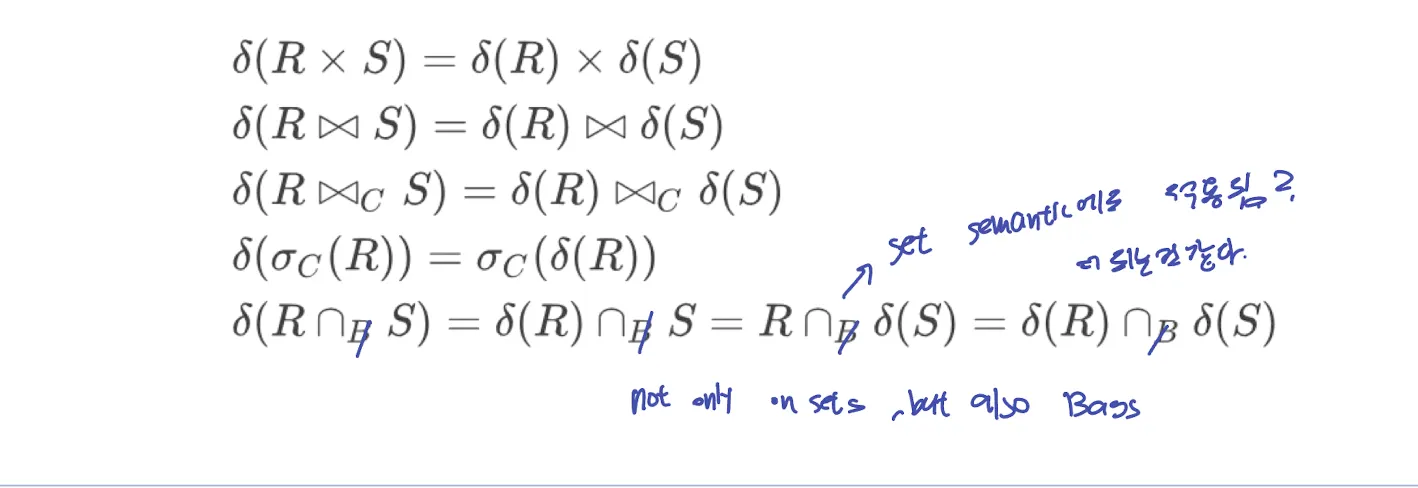Logical plan selection
Commutative and associative laws
•
조인, Union, Intersect에 대해서 모두 통한다.
•
set, bag semantics에 대해서도 통한다.
•
theta join은 communtative하지만 associative하지는 않을 수 있다.
Laws for selection
→ or에 대해서는 Set Semantic만 가능하다.
•
binary operator에 대해서는?
◦
C에 대해서 relation을 가지고 있는 친구들에게만 push down할 수 있다. 위 예시에선 R만 C 조건에 대해서 맞는 애들을 가지고 있다고 가정
◦
만약 둘다 C조건을 만족할 수 있다면 natural join인 경우에만 가능하다. 그냥 join이나 theta-join인 경우에는 적용이 안 되는데, 그건 shared attribute가 없기 때문. 반면에 Intersect는 또 되는데 그건 같은 scheme을 가지고 있기 때문.
Laws for projection
Laws about join and products
Laws for duplicate elimination
Laws for grouping and aggregation
Which transformation is good
•
일찍 뽑는게 기본적으로 좋다
•
projection and duplicate elimination은 조심히 다뤄야한다.
Physical plan selection
Estimate size of result
•
Size Parameter
•
Estimating projection
•
Estimating selection
•
Estimating join
•
Estimating Union, Intersect, difference, duplicate elimination, grouping
•
Obtaining estimate for size parameter
Estimate number of disk I/O
•
scanning tables
◦
sort-scan
▪
구현하는 방법은 여러개가 있다. R이 충분히 작다면 메인 메모리 알고리즘, 너무 크다면 multiway merge-sort 같은 걸 해야함.
◦
결과를 계산하기 위한 과정
▪
operator의 arguments들은 디스크에 있지만, 그 결과는 메인 메모리에 남는다고 생각.
•
Parameters for Measuring costs
◦
M: number of main memory buffers
◦
B: number of blocks, B(R)
◦
T: number of tuples, T(R)
◦
V: number of distinct values.
•
I/O cost for scan operators
◦
relation이 clustered 되있다면 disk I/O는 B이다.
◦
relation이 clustered 안 되어있다면, 훨씬 클 것이다. T이다.
◦
index-scan
•
One-pass algorithm
◦
메인 메모리에 arguments 들 중 하나가 들어가야한다.
◦
Tuple at a time, unary operations
▪
selection & projection
▪
relation이 메모리에 맞냐 안 맞냐와 상과없다.
▪
M ≥ 1
▪
cost: table-scan or index-scan of R
▪
clustered 되어있으면 B, 아니라면 T
◦
Full-relation, unary operations
▪
전체 relation에 대해서 적용해야하는 unary operation: 중복제거나 grouping
▪
중복 제거
•
처음 본 튜플이면 output에 복사를 해야함
•
전에 봤던 tuple이면 output으로 안 넣어도 됨.
•
B(중복제거(r)) ≤ M 이다.
▪
grouping
•
마지막 튜플을 보기 전까지 output을 생성할 수 없다.
•
disk I/O는 B이다.
•
M은 B랑 쉽게 관계가 찾아지진 않겠지만, 어쨌든 B보단 작을거야.
◦
Full-relation, binary operations
▪
Bag이냐 Set이냐로 나눌 거다.
▪
Bag union은 매우 간단한 one-pass algorithm으로 계산될 수 있다.
•
number of disk I/O : B(R)+B(S)
▪
다른 binary operation들은 one pass로 동작하려면 min(B(R), B(S)) ≤ M이다.
▪
정확하게 얘기하면 버퍼 한 개는 큰 relation의 block을 읽는데 사용되고, M buffer는 전체 크기가 작은 친구들을 읽는데 사용됨.
▪
Set Union
•
S를 M-1 buffer에 담은 다음, 모든 tuple이 search key가 되도록 search structure를 짠다. 그 다음 R의 각 block을 불러들여서, 모든 t에 대해서 S에 있는지 확인한다.
▪
Set Intersection
•
S를 M-1 buffer에 담은 다음, 모든 tuple이 search key가 되도록 structure를 짠다. R의 각 block을 읽어서 있으면 output, 없으면 무시한다.
▪
Set Difference
•
commutative 하지 않기 때문에 R-S랑 S-R을 구분해야한다.
•
R-S는 each R을 불러들여서 S에 있는지 확인하고 있으면 무시, 없으면 output
•
S-R은 each R을 불러들여서 S에 있으면 S에서 삭제 없으면 아무것도 아낳ㅁ.
▪
Bag Intersection
•
같은게 있다면 둘 중에 minimum만 뽑아야하기 때문에, count라는 값이 있어야한다.
•
이것 때문에 메모리가 살짝 더 필요할 순 있는데, approximation으로 B(s) ≤ M이면 충분
•
일단 S를 M-1에 불러놓고, count를 만든다.
•
R을 하나씩 불러들여서 있으면 count에서 하나를 까고 output, 아니면 아무것도 안 함
▪
Bag Difference
•
뭔지 잘 모르겠지만 어쨌든 불러들여서 비교하는 거임
▪
Product
•
S를 M-1에 불러놓고 R의 값을 하나씩 읽어서 붙이면 된다.
▪
Natural Join
•
R(X,Y)랑 S(Y,Z)랑 한다고 해보자.
•
S를 메인 메모리에 다 담고 Y에 대해서 search key를 설정하자. M-1 만큼 메모리로 사용
•
R의 각 블럭을 읽어들여서 매칭되는게 있으면 output으로 뽑음
▪
disk I/O : B(R) + B(S)이다.
•
Nested Loop Joins
◦
1과 1/2 pass이다.
◦
어떤 사이즈에도 적용이 되고, main 메모리에 맞을 필요가 없다.
◦
Tuple Based Nested Loop Join
▪
T(R) T(S)
◦
Block Based Nested Loop Join
▪
M만큼은 더 적은 Relation을 읽어들이는데 쓰고, 1만큼은 더 큰 relation을 읽어들이는데 씀
▪
B(S)/(M-1)(M-1 + B(R))
•
Two-pass algorithm
◦
일단 읽어서 뭔가 처리를 해서 disk에 쓰고, 이걸 읽어들여서 operation을 마치는 방식
•
ㄷTwo pass algorithm Based on Sorting
◦
Two-phase, Multiway Merge Sort
▪
M buffer로 R을 읽어들여서 정렬한다.
▪
sublist가 M-1개여야한다.
▪
B/M ≤ M-1이어야한다.
▪
전체 I/O는 3B
•
Duplicate Elimniation using sorting
◦
2PMMS처럼 main memory에 각 sublist마다 1block씩 하고 output block을 하나 해놓는다.
◦
하나를 뽑은 다음, sorted sublist에서 나타나는 block을 모두 제거하는 식
◦
따라서 disk I/O는 마찬가지로 3B(R)임
•
Grouping and Aggregation using sorting
◦
마찬가지로 정렬해서 하나씩 잡은 다음에 걔네들 중에 가장 작은 값이 그 다음 grouping value가 되는 식으로 처리
◦
3B(R), B(R) ≤ M^2
•
Sort based Union Algorithm
◦
bag-union의 경우에는 메모리 사이즈에 상관없이 동작하므로, one-pass algorithm을 쓰면 되는데, set-union의 경우에는 하나의 relation이 메인 메모리보다 작아야하므로 two-pass algorithm을 고려해야한다.
◦
disk I/O → 3(B(R) + B(S))
◦
B(R) + B(S) ≤ M^2
•
Sort based Difference Algorithm
◦
마찬가지이다.
•
Sort-Based Join
◦
5(B(R) + B(S))
◦
B(R) ≤ M^2 and B(S) ≤ M^2
◦
Improved sort-merge join
▪
정렬한거를 디스크에 다시 안 쓰고 안 읽으면 두 번씩 아낄 수 있다
▪
3(B(R) + B(S))
▪
B(R) + B(S) ≤ M^2
•
Two-Pass Algorithms Based on Hashing
◦
기본적으로 M-1과 1로 나눈다.
◦
M-1에는 R을 M-1개의 bucket으로 나눈 것들의 block을 하나씩 담고, 나머지 하나에는 R에 대한 블럭 하나를 담는다.
•
Hash Based Algorithm for Duplicated Elimination
◦
이 방법은 Ri가 메모리에 들어갈 정도로 충분히 작을 때 가능하다. 각 Ri bucket은 B(R)/M-1 블럭 사이즈여야한다.
◦
그래야 B(R) ≤ M(M-1) 이 된다.
◦
전체 disk I/O 는 3B(R)임.
•
Hash Based Grouping and Aggregation
◦
비슷하게 M-1 bucket으로 전부다 hashing
◦
B(R) ≤ M^2
◦
3B(R)
•
Hash Based Union, Intersection, Difference
◦
각각 M-1 bucke으로 만들어야한다.
◦
B(R)/M-1과 B(R)/M-1)이 M보다 작아야하므로 min(B(R),B(S)) ≤ M^2이다.
◦
disk I/O : 3(B(R) + B(S))
•
Hash-Join Algorithm
◦
disk I/O : 3(B(R) + B(S))
◦
memory: min (B(R),B(S)) ≤ M^2
•
Hybrid Hash join
◦
S에 대해서 k개로 hashing하기.
◦
k개 중에 m개를 골라서 메모리에 완전히 올리기, 다만 나머지 k-m개에 대해서는 1block씩 남겨놓은 상태로
◦
m B(S)/k + k-m ≤ M
◦
만약 R을 읽었는데, m개 중에 하나로 hashing이 된다면, 그냥 바로 조인하면 된다.
◦
한 번 성공할 때마다 2번 I/O를 아끼는거니까 2(m/k)(B(R) + B(S))만큼 아껴진다.
◦
결론이 뭐냐 m=1이고 k를 낮출 수 있는 만큼 낮춰라.
◦
k = B(S) / M이다. 대입하면 2M(B(R) + B(S))/B(S)
◦
따라서 total cost는 (3-2M/B(S))(B(R) + B(S))이다.
•
Index Based Algorithm
◦
S had an index on join attribute Y
◦
클러스터링은 같은 Y값에 대해 뭉쳐있으면 클러스터링됬다고 한다.
◦
클러스터링된걸 찾을 때는 B(S) / V(S,Y)이고 클러스터링 안 될걸 찾을 때는 T(S)/V(S,Y)이다.
◦
join cost는 clustering 안 되면 B(R) + T(R)T(S)/V(S,Y), clustered 되면 B(R) + T(R)(max(1,B(S)/V(S,Y))
•
Zig-zag join using ordered indexes
◦
B-tree indexes에 있으면 그냥 tree의 leaf를 scan하면 된다.
.jpg&blockId=1b87074d-017e-8069-9667-d5678d39e51d)