Node Embeddings

Node Embeddings 요소

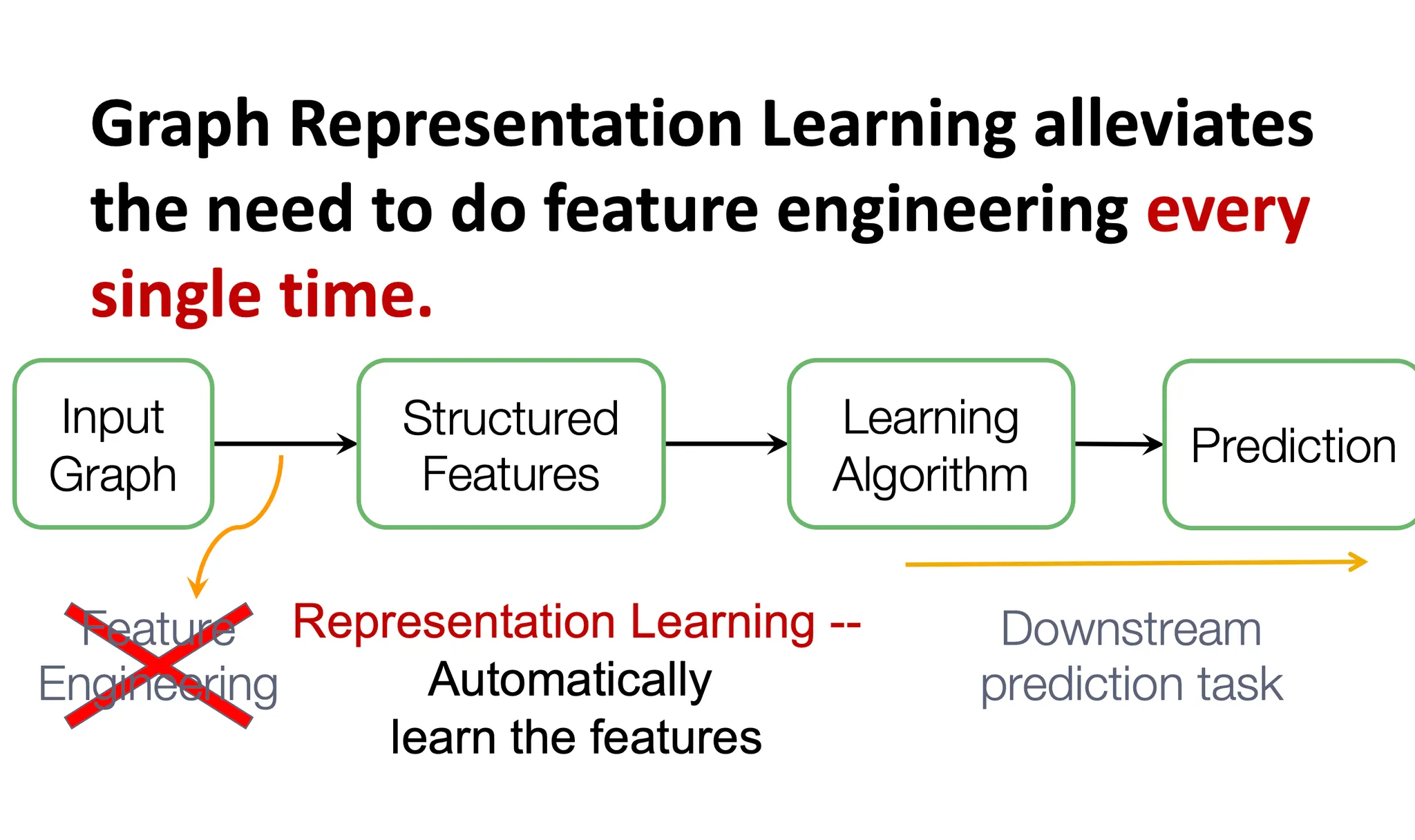
Graph Representation Learning은 Graph를 Input으로 받아서 structured feature를 만들고 이를 알고리즘에 집어넣는 과정에서 feature engineering 과정을 없앤 것입니다. 우리가 데이터를 가공할 때 feature engineering을 거치듯 graph의 경우에도 해당 노드를 나타내는 여러 feature들이 있을 수 있습니다. 누구와 연결되었냐부터 degree는 몇 인지, node 자체에 텍스트나 이런 정보는 있는지 등등이 될 수 있습니다.

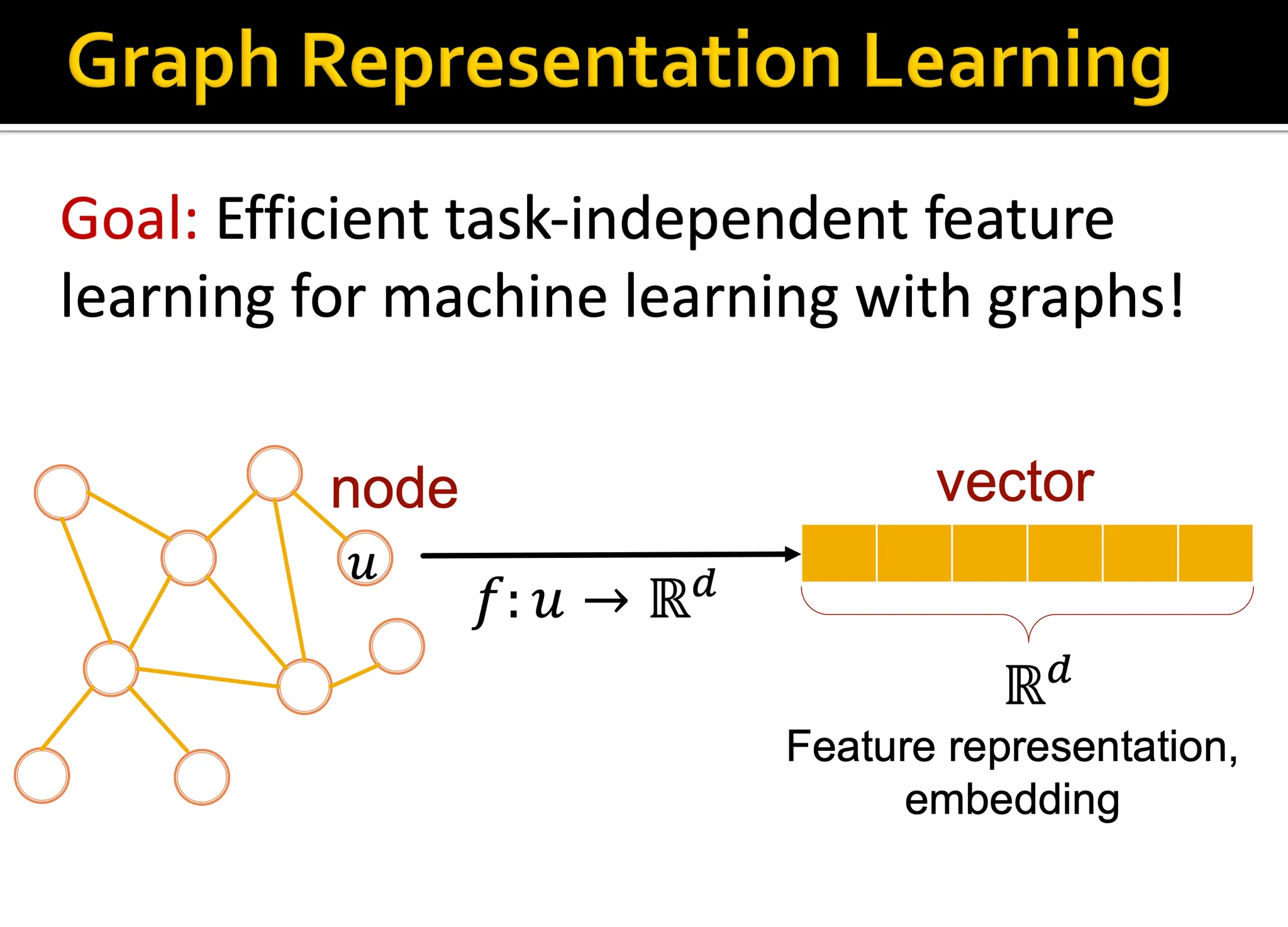
Graph Representation learning은 결국 이런 feature engineering의 과정을 거치지 않고, downstream task에 가장 적합한 벡터로 각 노드를 변환시키는 과정을 의미합니다. 이 단원에서 얘기하는 node embedding 방법은 결국 random walk 기반의 방법들인데, 이 방법 외에 Deep learning을 이용한 방법 등 더 많은 내용이 뒤에 소개될 예정입니다.

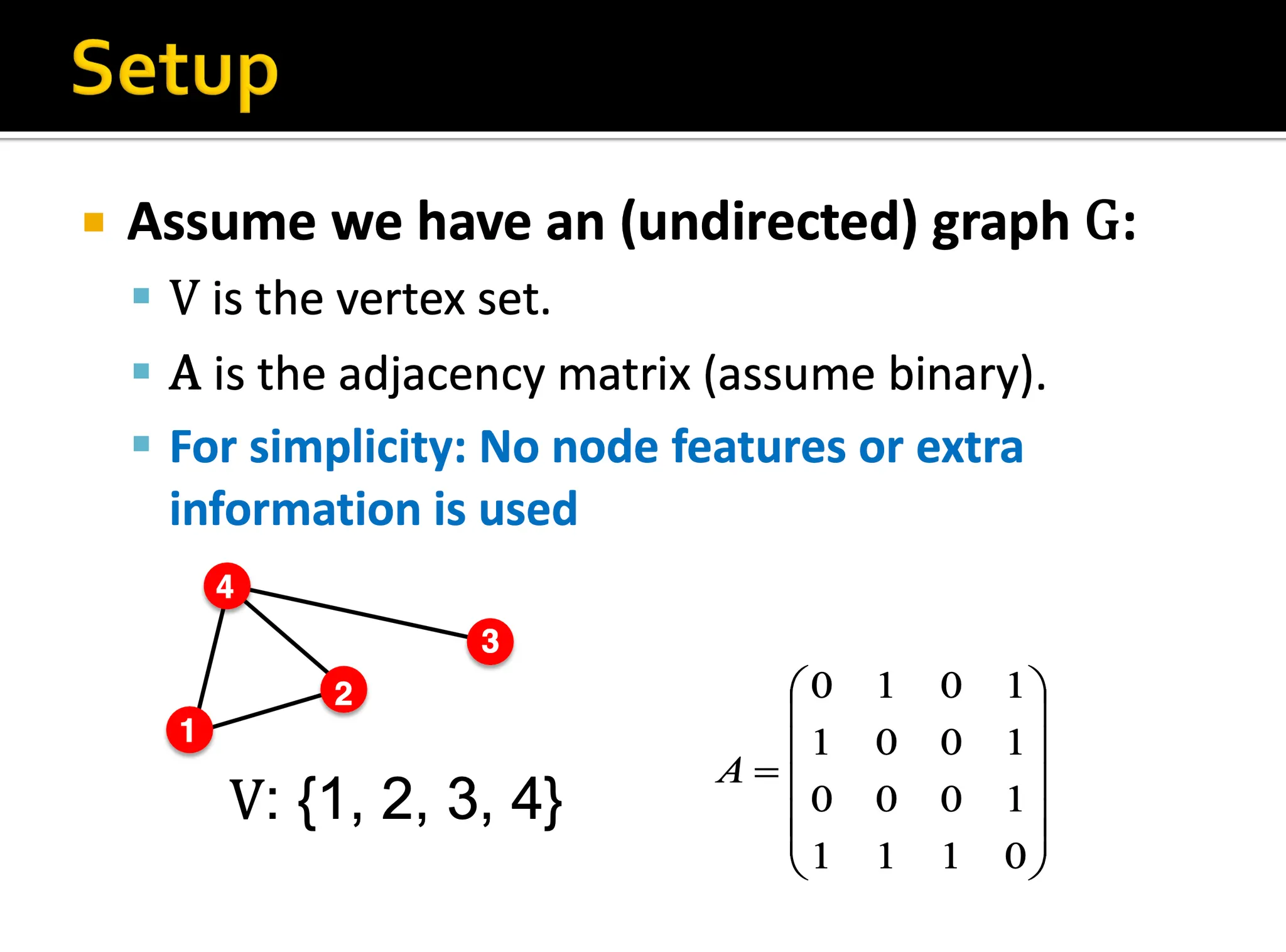
문제를 단순하고 잘 정리하기 위해서 추가적인 feature는 사용하지 않고 오직 어떻게 연결되어있나만을 고려합니다. 우리의 목표는 이 그래프의 구조를 잘 반영한 각 노드 임베딩을 만들어내는 것입니다.

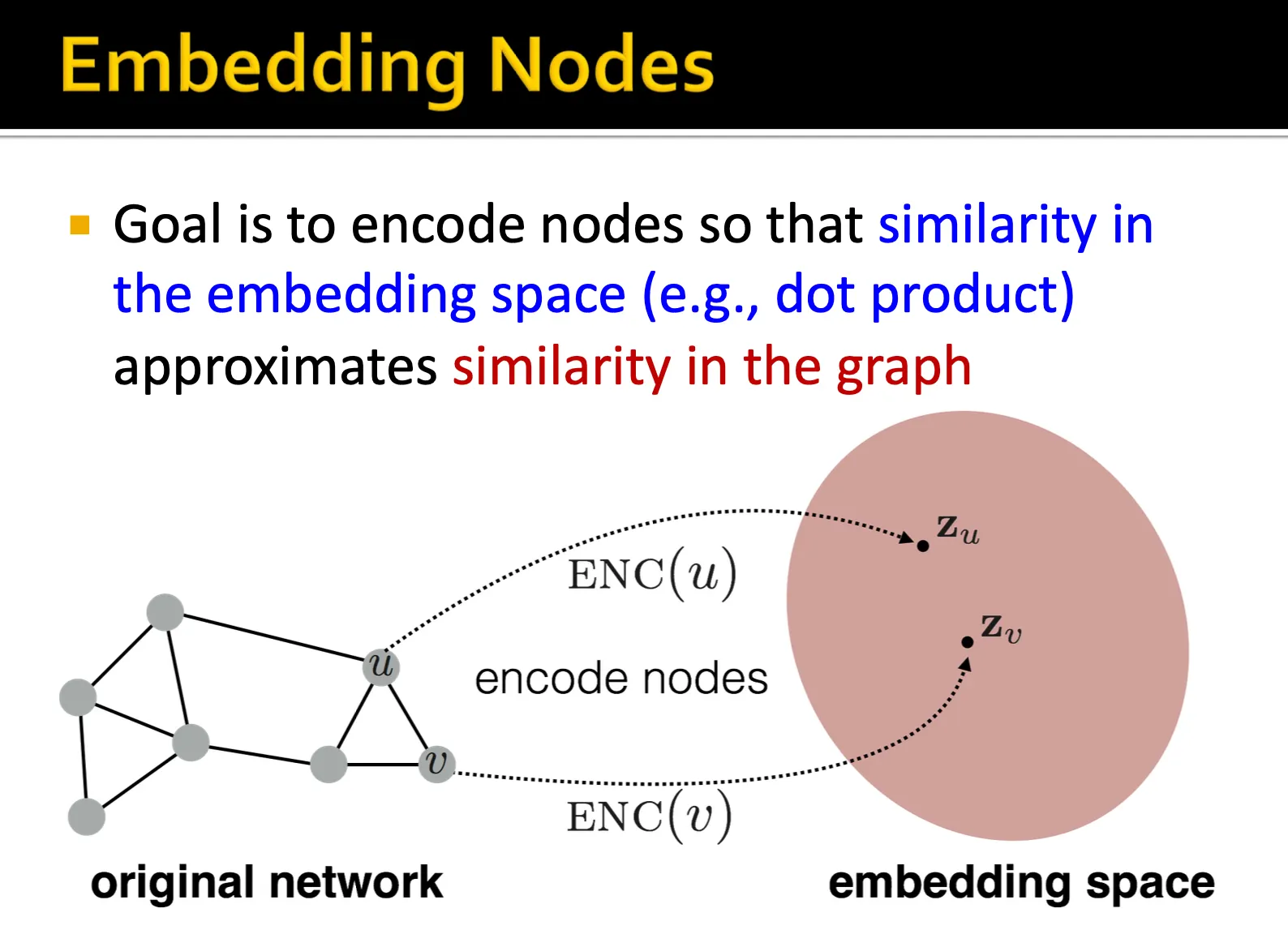
이 과정에서 총 3가지의 component가 정의됩니다. - Encoder, Decoder, Similarity function 입니다.

Encoder는 각 노드를 embedding space로 바꿔주는 역할을 하고, similarity function은 네트워크 상에서 유사도를 어떻게 정의할 것인지를 의미합니다. Decoder는 embedding들을 similarity score로 바꿔주는 역할입니다. 위 페이지에서 이미 Decoder는 정의가 된 상태입니다. 임베딩 간의 dot prodoct로 similarity score를 계산하기 때문에 Decoder는 dot product 연산이 됩니다. dot product 연산 외에도 거리 함수로써 다양한 함수들이 사용될 수 있고, Metric Learning과 같이 sampling을 기반으로 label을 가장 잘 분리해낼 수 있는 거리 함수를 학습하는 경우도 있기 때문에 Decoder 또한 정의되고 학습 될 수 있습니다.

Encoder의 경우, 현재 노드의 추가적인 feature를 전혀 사용하지 않기 때문에 ‘Shallow’ Encoding이라 부르고, 그저 embedding look-up 함수로 정의할 수 밖에 없고, 정의해도 충분합니다.

여기서 우선 개념적으로 가장 중요한 것은 similarity function 입니다. 우리가 그래프 상에서 유사하다를 어떻게 정의할지에 따라 임베딩 공간에서의 유사도도 동일하게 정렬될 것이며, 이를 통해 추가 downstream task에 활용할 것이기에 어떻게 node similarity를 정의할 것이냐가 굉장히 중요한 문제입니다.

여기서는 random walk로 정의한다고 합니다.

Random Walk (Deep Walk)

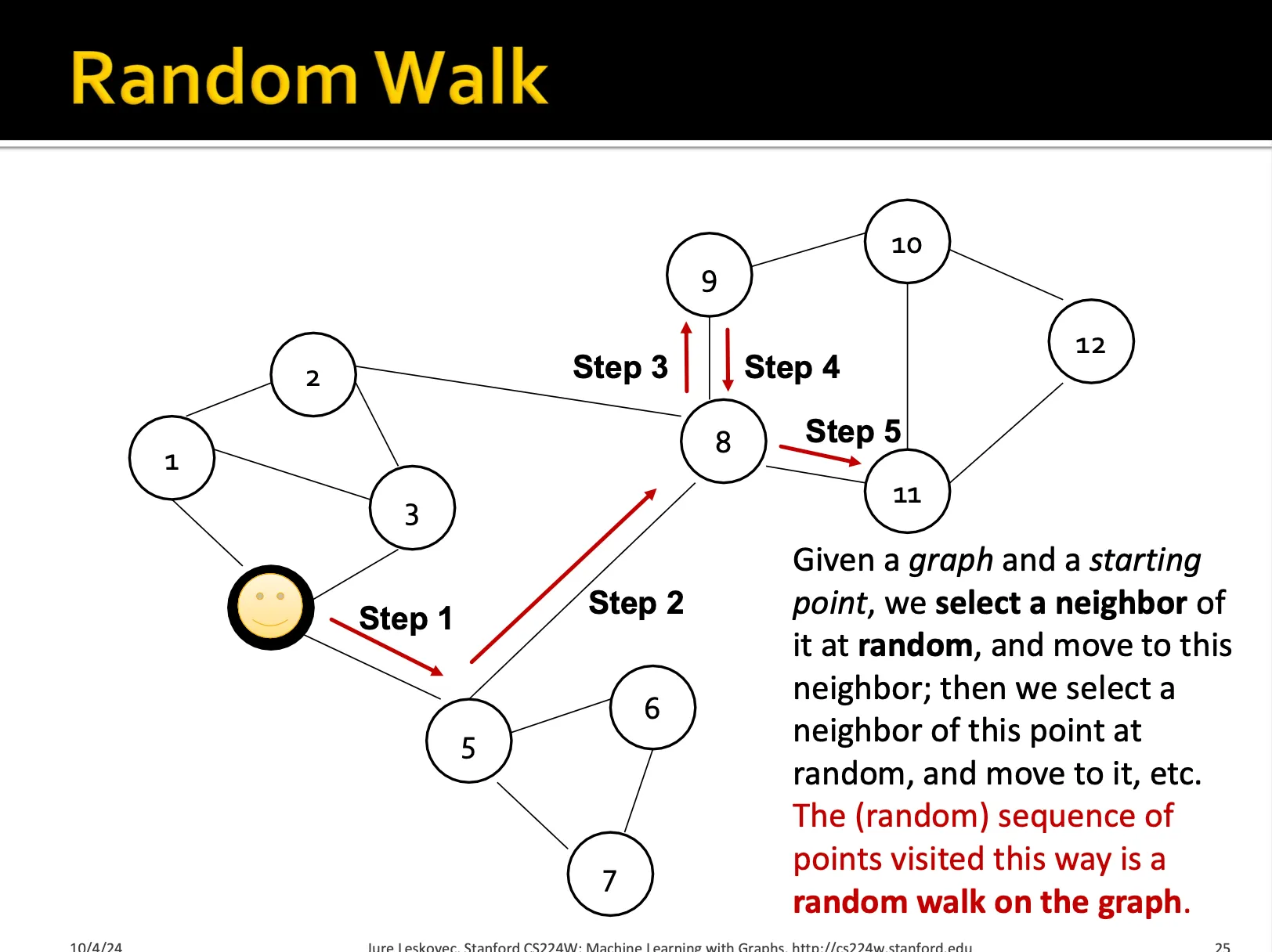
random walk는 특정한 노드에서 출발해서 특정한 길이의 sequence를 랜덥하게 움직이는 방법입니다.

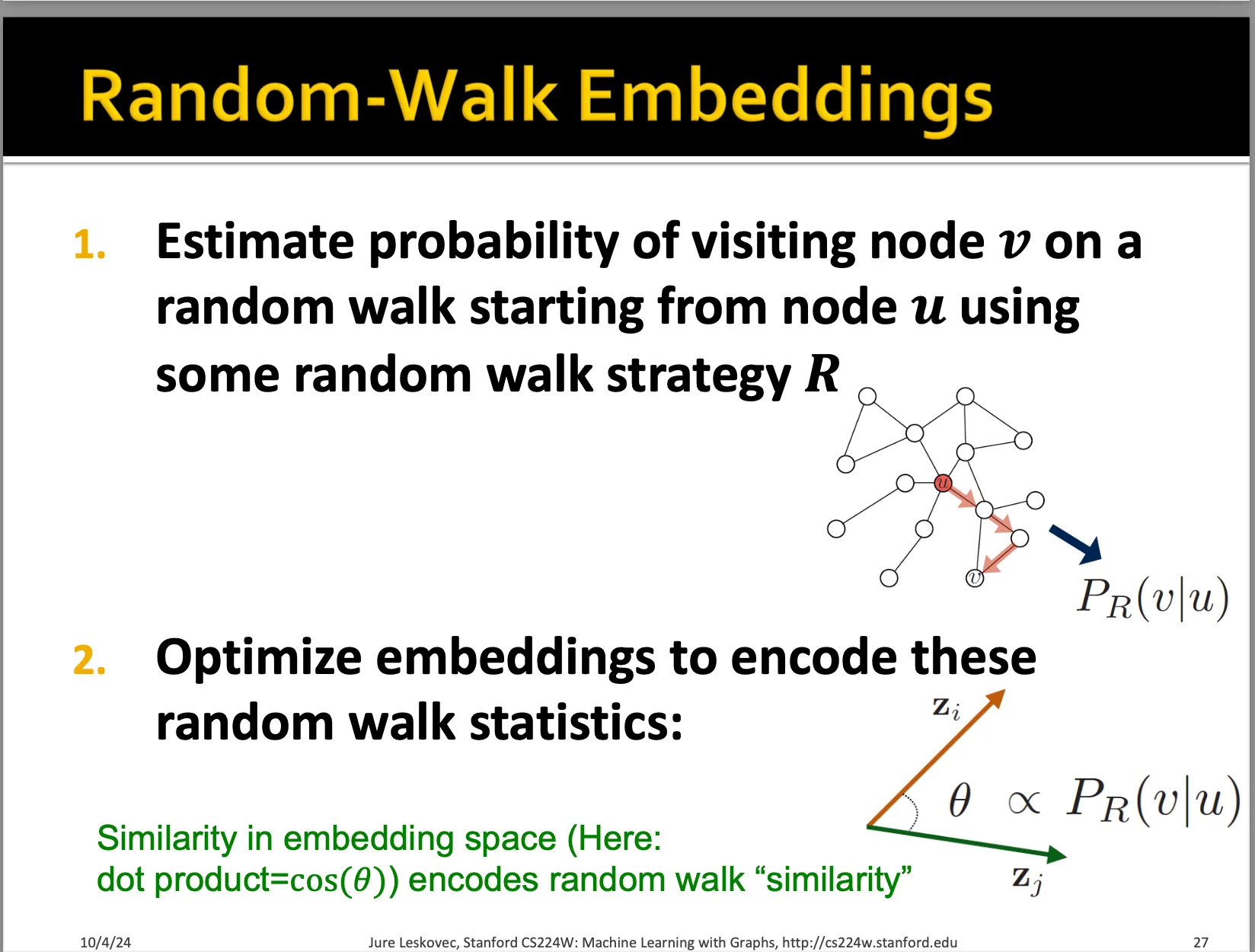
우리는 random walk를 많이 수행하였을 때, 각 노드에서 다른 노드로 이동하는 확률을 추정할 수 있을 것입니다. 그 확률이 높은 것을 유사도가 높다라고 얘기하고, 이를 학습하는 embedding을 만들고자 합니다.

random walk는 stochastic한 방법입니다. 즉, 확률적인 방법으로써 매번 시행할 때마다 결과가 달라집니다. 이를 통해 획득한 노드 간 이동 확률을 similarity가 높다고 얘기하는 것은 직관적으로 맞는 말인 것 같습니다. 부가적으로 이 방법은 각 노드가 local과 high-order neighborhood information을 모두 학습하게 해줍니다.

구체적인 formulation은 다음과 같습니다.

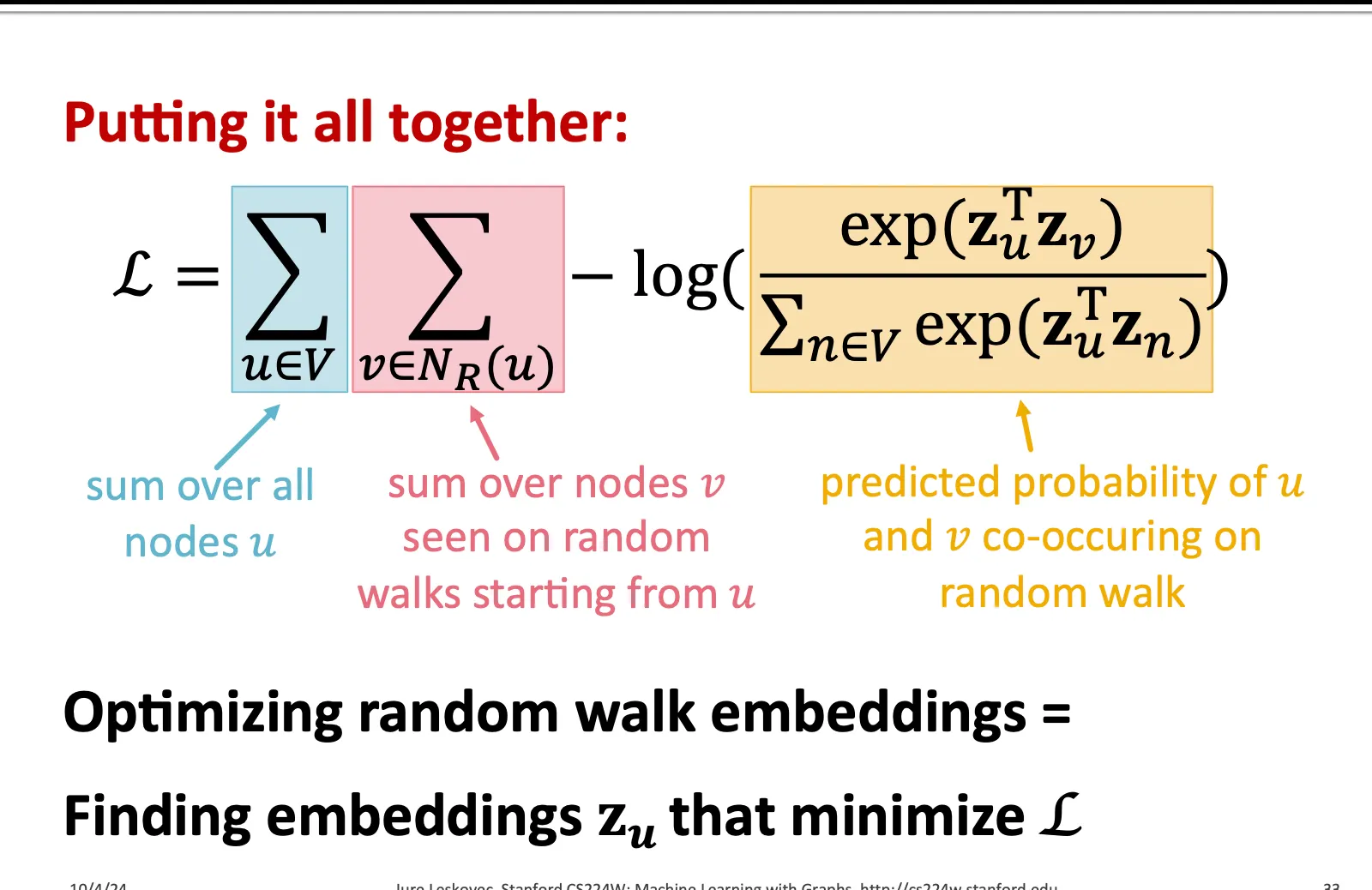
우선 node u에 대한 임베딩이 주어졌을 때, 그것과 유사한 이웃들 N_R(u)를 잘 예측하는 것이 목적입니다. 이는 seq2seq에서 skip-gram이라고 불리는 방법인데, 하나의 시퀀스 내의 단어가 주어졌을 때 주변 단어들을 예측하는 방식입니다.

현재 우리는 여러 번의 random walk를 시행해서 여러 개의 node sequence를 가지고 있고, 이를 통해 node u의 neighborhood를 찾을 수 있습니다. 그리고 우리는 현재 random walk 상에서 한 노드에서 다른 노드로 이동할 확률을 유사도로 정의하고 이를 학습할 수 있는 방식을 찾고 있습니다. 따라서 random walk에서 한 노드에서 시작해서 나온 sequence를 neighbor라고 정의하고, 그래프 상 모든 노드에 대해서 이 neighbor들을 분류하는 방식으로 loss function을 설계한다면 우리가 원하는 바를 달성할 수 있습니다.

Negative Sampling

다만 위와 같은 계산은 너무 비쌉니다. 왜냐하면 그래프 상 모든 node에 대해서 iteration을 하게 되고, 이 때 현재 u를 target node라고 하면, 이 target node가 주어졌을 때, 다시 그래프 상 모든 node에 대해서 softmax를 계산해야하기 때문에 총 연산량은 V^2가 됩니다.

이를 통해 softmax를 계산할 때, 모든 node를 계산하는 것이 아니라, negative sample을 설정하여 그것들과의 유사도는 낮게, target node가 실제로 건너온 node들과는 유사도가 높게끔 함수를 만들어주면 됩니다.

이것이 동작하는 직관적인 원리는, softmax 함수 자체가 합해서 1이 되는 함수이기 때문입니다. 모든 값이 다 같이 높아질 수도, 다 같이 낮아질 수도 없고, 한 값이 높아지면 한 값은 무조건 낮아져야합니다. 따라서 현재 node u의 neighbor들에 대해서 softmax를 계산해서 loss에 사용하고 있는데 이는 필연적으로 neighbor가 아닌 값들의 similarity는 낮아지게 만듭니다. 그렇다면 우리의 목표는 neighbor들의 값만 높아지게 하면 되는 것이기 때문에 분모에서 모든 node에 대해 similarity를 계산하는 것이 아니라, 특정한 negative sample만 추출하여 그 값에 대해서는 낮아지고 다른 값에 대해서는 높아지게끔만 해도 같은 효과를 얻을 수 있습니다.

Node2Vec

현재는 unbiased 된 방식으로 random walk를 하지만, 특정한 방식으로 random walk를 해도 되지 않을까요? 그것이 바로 node2vec입니다.

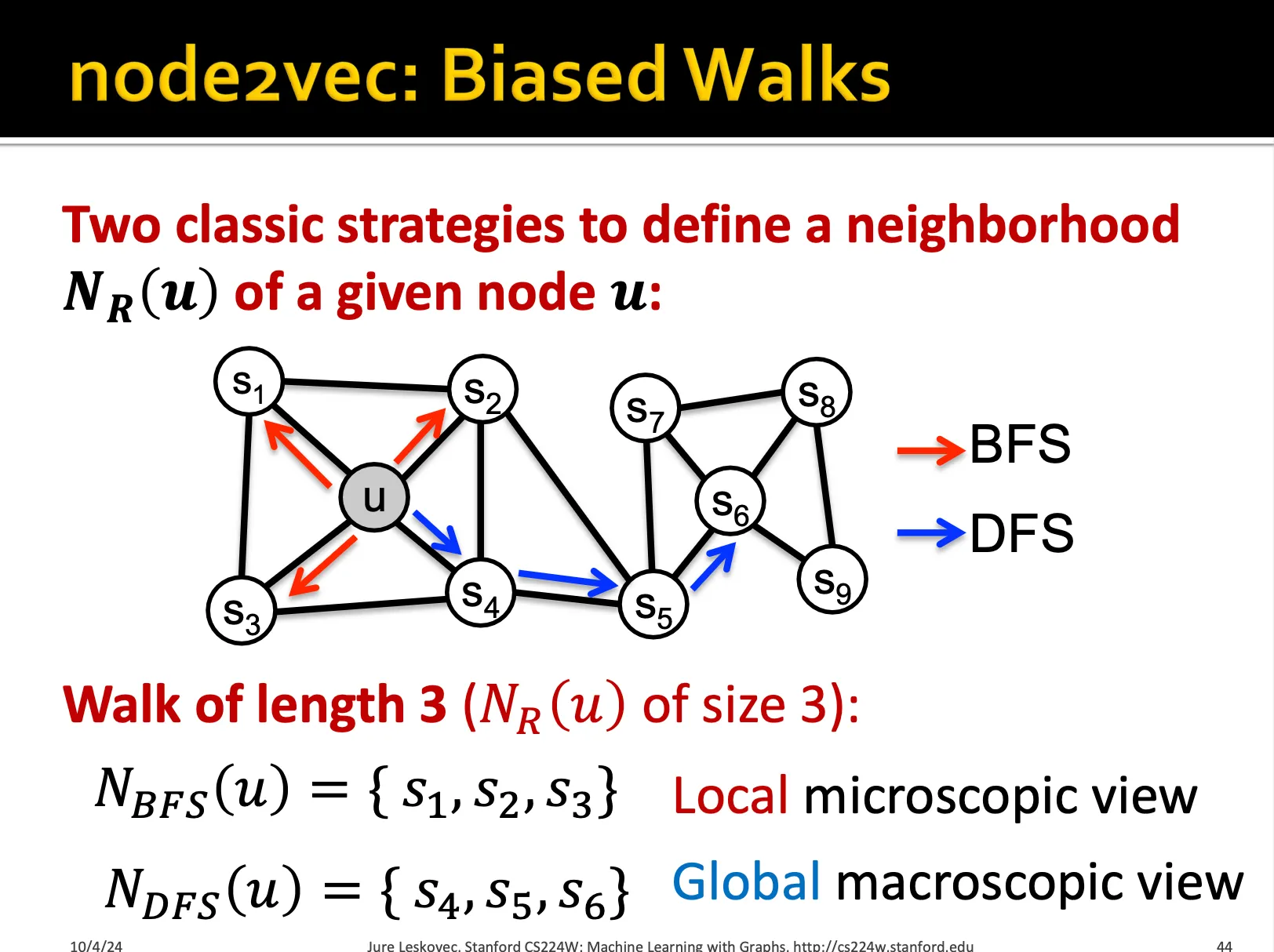
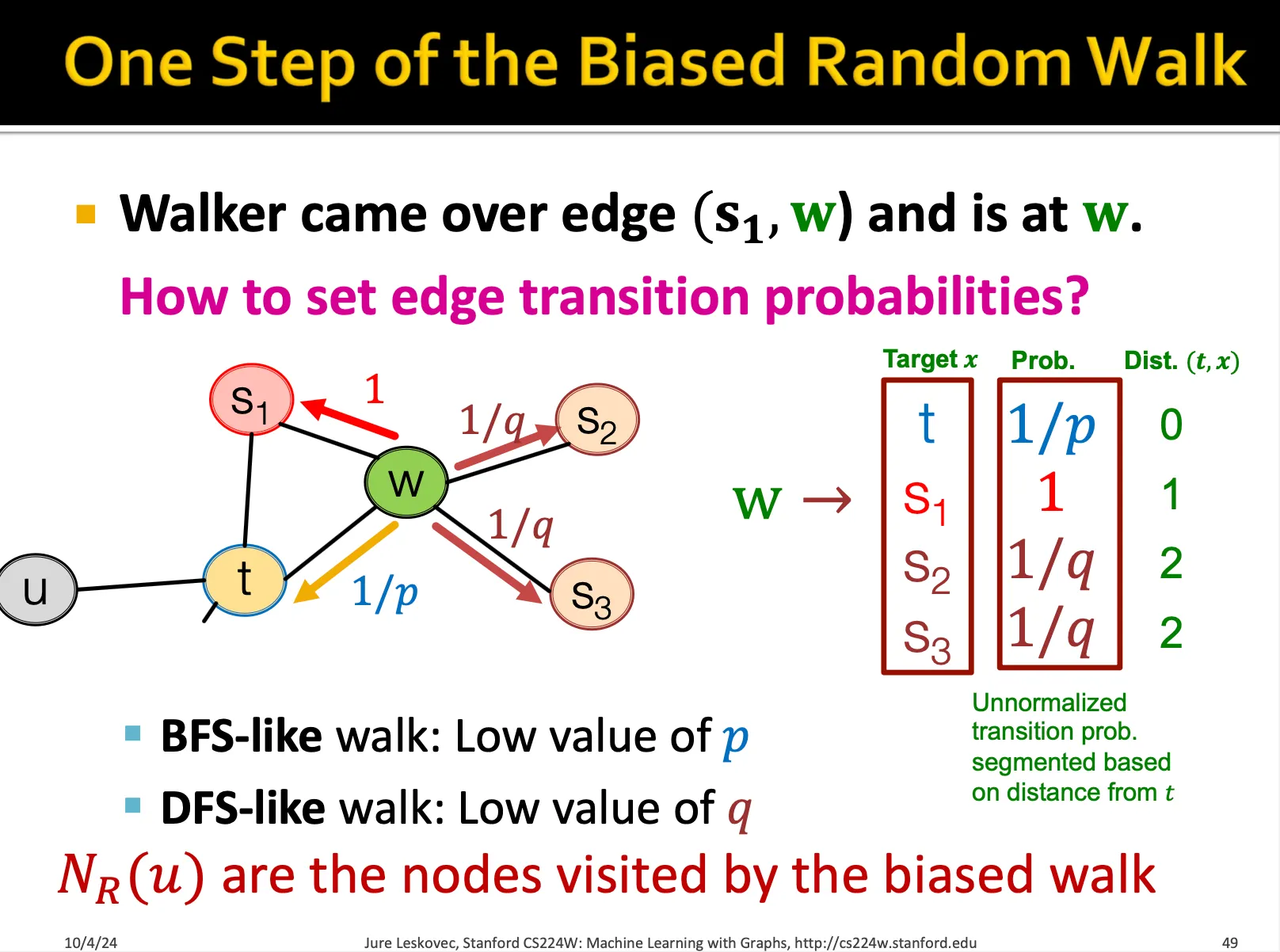
node2vec 방식에서는 BFS와 DFS 2가지 방식이 존재합니다. 그리고 이를 조절하는 p와 q 확률이 존재합니다.

t,w 로 이어지는 walk를 수행하고 있을 때, 즉 지금 w에 존재할 때, 다시 t로 돌아갈 확률이 1/p, t랑 같은 거리에 있는 노드로 이동할 확률을 1, 더 멀어질 확률은 1/q로 설정해서 나아갑니다. 물론 이 값은 모두 normalize 되야합니다.

해당 알고리즘은 biased 된 random walk로써 파라미터로 global한 뷰 또는 local 뷰를 학습하거나를 조절할 수 있다는 장점이 있습니다. 또한 아래 세 가지 step으로 이루어지는데 각 step은 모두 병렬로 연산이 가능합니다.

probability도 모든 next node에 대해서 병렬로 연산이 가능하고, simulate하는 경우도 r 번의 random walk를 병렬로 연산이 가능하며, 이렇게 획득한 sequence를 SGD로 병렬로 연산이 가능합니다.

뿐만 아니라 각 method별로 어떻게 similarity를 정의하는지가 다르기 때문에 잘 수행하는 task도 다른 것 같습니다.

Matrix Factorization

node u,v가 similar할 때 연결된다고 생각해보면 우리는 A 행렬이 그 유사도를 가장 잘 나타내고 있다고 생각할 수 있습니다. 따라서 이를 잘 행렬 분해를 한다면 ‘연결될지’를 나타내는 임베딩을 획득할 수 있지 않을까하는 생각입니다. 완벽하게 분해할 수는 없기에, 그 차이를 최소화하는 방향으로 학습하고자 합니다.

이 섹션에서 특이한 점은 random walk 같은 경우에도 matrix factorization과 같은 방식의 유사도를 반영한다고 얘기할 수 있다는 것입니다.

Limitation

transductive method 입니다.

새로운 노드에 대해서는 임베딩을 획득하지 못합니다.

따라서 새로운 노드가 나타나면 그래프에 대해서 새롭게 임베딩을 구해야합니다.

구조적인 유사성을 학습하지 못합니다.

그래프의 구조적인 유사성을 학습하지 못합니다.

얼핏 알고 있는 WL-test 에 사용되는 그래프 모양을 반영하지 못합니다.

node, edge, graph feature를 활용하지 못합니다.